Folgende Aufgabe lässt mich verzweifeln:
Für die Erzeugung eines Produktes lautet die Grenzkostenfunktion K'(x)=0.075x^2-1.64x+12.52
Die Fixkosten betragen 91.85 GE.
Für die lineare Absatzfunktion p(x)=kx+d gelten folgende Gesetze: Bei einem Absatz von 5 ME lässt sich ein Preis von 30 GE erzielen, bei einem Absatz von 15 ME ein Preis von 20 GE. Stellen Sie die Gleichungen der Gesamt-Kostenfunktion K(x) und der Absatzfunktion p(x) auf und bestimmen Sie die gewinnmaximierende Menge und den maximalen Gewinn.
1) Ich zeichne also in Geogebra die Funktion K'(x)= 0.075x^2-1.64x+12.52+91.85
2) Ich integriere K'(x) in 0.03x^3-0.82x^2+104.37x
3) Ich mache zwei Punkte A=(5,30) B=(15,20) und ziehe die Gerade dadurch.
4) Gerade ergibt x+y=35, um p(x) zu erhalten multipliziere ich ein x dazu : 35-x, da die Gerade ja nach unten zeigt.
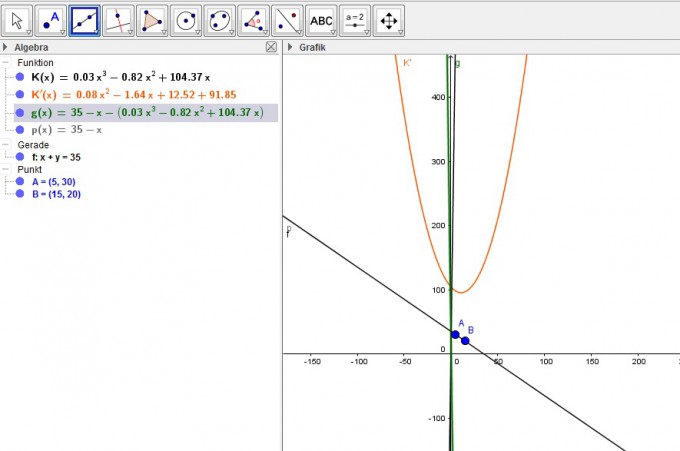
5) Ich subtrahiere p(x) - K(x) = ergibt hier im Bild g(x), was natürlich nicht stimmen kann...
Findet ihr eventuell meinen Fehler? Ich lade die Geogebra Datei und ein Bild hoch.
 übungen.ggb (8 kb)
übungen.ggb (8 kb)