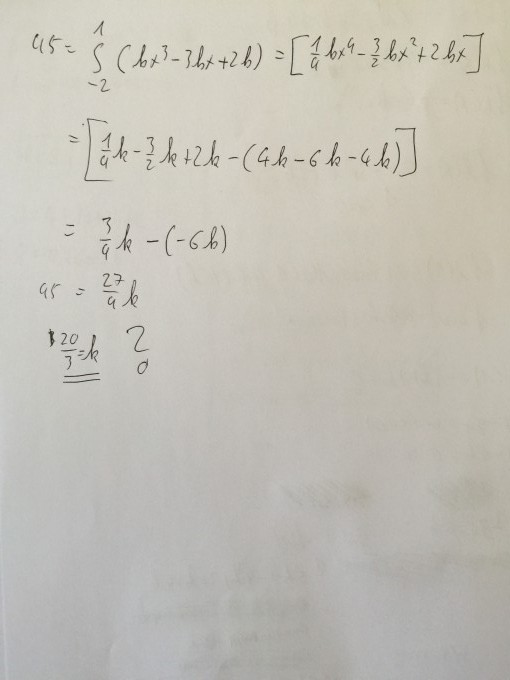Steckbriefaufgabe und Kurvendiskussion. f_(k)(x) = k(-x^3 + 3x + 4).

Question

Wie löst man diese etwas komplexeren Aufgaben?

Ich bräuchte hier mal etwas Hilfe bei diesen zwei Aufgaben. Die Nummer 5 habe ich schon gelöst, hierbei besteht nur die Frage ob dies auch richtig ist und warumdas weglassen von k bei der Polynomdiv. möglich ist. Bei der Nummer 6 ist ein Lösungsansatz vorhanden, aber es hängt beim Integral bzw. beim herausfinden der Grenzen.

Vielen Dank schon im Voraus

Lg Sebastian EDIT: Fragetext aus Kommentar: 

Comments

Günstig wäre es wenn du die original Aufgaben auch mit dazu schreibst. Dann kann man das durchrechnen und du kannst dann vergleichen.

---

Oh, das wurde anscheinend nicht mit hochgeladen sorry

Answer 1

5.

f(x) = k·(- x^3 + 3·x + 4)

f'(x) = 3·k·(1 - x^2) = 0 --> x = 1 (Hochpunkt) ; x = -1 (Tiefpunkt)

f(1) = 6·k

f(x) = k·(- x^3 + 3·x + 4) = 6·k --> x = -2 ; x = 1

∫ (-2 bis 1) (6·k - k·(- x^3 + 3·x + 4)) dx = 27/4·k = 45 --> k = 20/3

Da komme ich auf dein Ergebnis. Sieht also gut aus.

Comments

6.

f(x) = x^4 + a·x^3 + b·x^2 + c·x + d

f(0) = 1 --> d = 1

f'(0) = 0 --> c = 0

f''(0) = 0 --> 2b = 0 --> b = 0

f(x) = x^4 + a·x^3 + 1

Schnittstellen f(x) = 1

x^4 + a·x^3 + 1 = 1 --> x = 0 ; x = - a

∫ (-a bis 0) (x^4 + a·x^3 + 1 - 1) dx = - a^5/20

| - a^5/20| = 5000

a = ± 10

---

Ach was bin ich dämlich danke schön :)