Limes von Bruchtern mit Gauss-Klammern 'x√(2n)' /√(2n -' x√2n'))

Question

Aufgabe:

Bruchtern mit Gauss-Klammern berechnen:

$$ \lim _ { n \rightarrow \infty } \frac { \lceil x \sqrt { 2 n } \rceil } { \sqrt { 2 n - \lceil x \sqrt { 2 n } \rceil } } = x $$

Ich komm nicht drauf, dass das gegen x gehen soll.

Mein Tipp wäre das Sandwichtheorem, aber die Gauß-Klammern sind echt ein Problem. Ich weiß nicht, wie abschätzen, damit die rausfliegen. Hat jemand einen Tipp für mich?

Comments

der Ausdruck ( im Zähler in der Wurzel )

lim n -> ∞ [ 2 * n - x * √ (2 * n ) ]  = 2 * n

( Einfaches Beispiel : lim a -> ∞ [ a - √ a ]= a . Die Differenz zwischen a  und √ a
wird immer größer und geht gegen unendlich ).

Der gesamte Term reduziert sich dann zu

x * √ (2 * n ) /  √ (2 * n ) = x

mfg Georg

Ohne Gewähr. Bei Fehlern oder Fragen wieder melden.

---

Die Differenz zwischen a  und √a wird immer größer und geht gegen unendlich.

Damit ist der Grenzwert aber nicht a!

---

Vorschlag: Ersetze ⌈x·√(2n)⌉ im ganzen Term
durch x·√(2n) für eine Abschätzung nach unten bzw.
durch (x·√(2n)+1) für eine Abschätzung nach oben.

---

Hallo anonym,

" Damit ist der Grenzwert aber nicht a! "

a - √ a
√ a * √ a  - √ a
√ a * ( √ a  - 1 )
lim a -> ∞ von ( √ a - 1) = √ a
also bleibt
√ a * √ a
a

mfg Georg

---

Der Grenzwert kann nicht a sein, denn a läuft gegen Unendlich. Man kann allenfalls daraus schließen, dass a-√a bestimmt gegen Unendlich divergiert. Aber hilft das hier weiter?

---

ich habe 2 Funktionen

a.) f(a) = √ a

b.) g(a) = √ a - 1

Jetzt zeichne ich mir einmal den Graphen der beiden Funktionen.
Die Funktion b.) nähert sich immer mehr a.) an. Ich denke schon das
meine Aussage

lim a -> ∞ von ( √ a - 1) = √ a

stimmt.

mfg Georg

---

vielen dank für die antworten :-) ich denk mal über eure vorschläge nach :-))

wenn ichs so gelöst habe, kann ichs ja mal posten :-)

---

Ich denke schon das meine Aussage lim a -> ∞ von ( √ a - 1) = √ a stimmt.

Hallo Georg! Auf der rechten Seite steht nun kein Wert mehr, mit dem man rechnen könnte, sondern Unendlich. Deine Argumentation scheint für mich darauf hinauszulaufen, dass Du zunächst die Grenzübergänge im Zähler und im Nenner durchführst und dann den Faktor "Unendlich" herauskürzt. Welcher Grenzwertsatz erlaubt das denn?

---

Hallo anonym,

" Auf der rechten Seite steht nun kein Wert mehr, mit dem man rechnen könnte, sondern Unendlich. "

  Dann fasse ich mal meine Überlegungen in Worte.

  Im Nenner steht in der Wurzel der Term

  2 * n - x * √ (2 * n ). Diesen forme ich um in

  √ (2 * n ) * √ (2 * n ) - x * √ (2 * n )
  √ (2 * n )  * (  √ (2 * n ) - x  )

  Für den Fall das n gegen unendlich geht reduziert sich der Term

  √ (2 * n ) - x   auf   ( das x wird völlig unbedeutend )
  √ (2 * n ) ( den Term könnte man als Asymptote von √ (2 * n ) - x auffassen )

  und

  √ (2 * n ) * √ (2 * n ) - x  ) wird zu
  √ (2 * n )  * √ (2 * n )
   2 * n

  Die gesamte Funktion
f(x) = x * √ (2 * n  / ) √ (2 * n - x * √ (2 * n ))

reduziert sich auf

   f(x) =  x * √ (2 * n ) /  √ (2 * n )
   f(x)  = x

  Das Ergebnis x wurde überprüft und stimmt.

  Ich habe mir Differntial- und Integralrechnung in den letzten Jahren
autodidaktisch beigebracht. Eine große Hilfe war die Webseite
w w w . a b i t u r l ö s u n g  . d e. Dort werden die Abiturarbeiten von Bayern
der letzten Jahrzehnte von Lehrern u.a. als Video besprochen.

  Ich denke, bei dieser Aufgabe wäre das Vorgehen der Lehrkraft nicht
anders gewesen als wie hier dargestellt.

  Solltest du eine andere Herangehensweise haben teile sie doch bitte mit.

  mfg Georg

---

So hallo nochmal :D

zu dem thema nach unten und oben abschätzen... hab ich ein Problem wenns nach oben geht!

Wenn ich mit dem, was im Nenner steht erweiter, geht die wurzel unten weg und im Zähler kann ich die Wurzel ja auch weglassen, weil es ja größer werden soll... Kürzen und es bleibt x wurzel 2 n + 1 übrig... nur kein x ... wie schätzt du ab??

 

zu Georg: Ich glaaauuubbeee ich weiß, wie du meinst, das muss ich aber noch ordentlich aufschreiben und mal schauen, ob ich da auch auf ein Problem stoße :-)

Trotzdem echt nett von euch, dass ihr mir so helft!!

---

Zur Abschätzung nach unten: Das kannst Du so nicht machen, denn x kann auch negativ sein. Ziehe 2n aus der Wurzel heraus und kürze dann. Dies funktioniert auch bei der Abschätzung nach oben.

---

sorry ich komm grad nich ganz mit... wie kann man des 2n rausziehen?

also wir reden vom nenner... oder? :D

und da vom hinteren wurzel 2n...?? und das soll aus der großen wurzel im nenner raus?

geht das überhaupt?

---

Du klammerst zunächst 2n im Radikanden der äußeren Nennerwurzel aus und ziehst das dann als sqrt(2n) aus der Wurzel. Anschließend kannst Du kürzen.

---

jetzt bin ich total verwirrt...

 

was bringt mir das jetzt???

oder kannst dus mal hinschreiben wie dus meinst? dann probier ichs bei der abschätzung nach oben nachzumachen...

---

Ja, so habe ich das gemeint! Das Blaue kürzt sich weg und der Nenner wird beim Grenzübergang zu eins. Was verwirrt Dich daran?

---

wieso wird der nenner 1??

---

sqrt(1-x*sqrt(2n)/(2n)) = sqrt(1-x/sqrt(2n)) -> 1

---

also müsste x/sqrt(2n) null sein aber nur n läuft ja gegen unendlich... x bleibt fix... wie kommst du da auf null??

---

Das ist dasselbe wie bei 1/x für x gegen Unendlich...

---

ok dann ist alles klar, was die abschätzung nach unten angeht^^

viiieeelleennn dank!!

 

jetzt zur abschätzung nach oben:

da sagst du ja, es würd gleich gehen...

aber dieses +1 stört doch total? kannst du mir da bitte nochmal einen tipp geben?

 

 

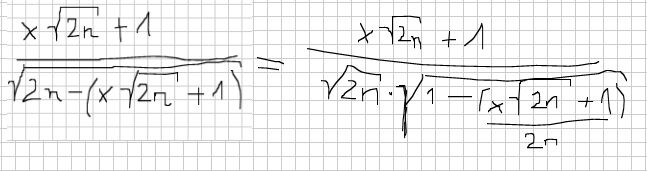
also kürzen geht so ja echt schlecht... was bringt jetzt das ausklammern? ok ich kann den bruch außeinanderziehen und vorne dann x/große wurzel stehen haben + 1/alles von unten

letzteres könnte ja wieder eine nullfolge sein (oder?) aber das vordere??

(sorry dass ich so spät noch damit nerve :D mich hat jetzt total der ehrgeiz gepackt xD)

---

Richtig, Bruch zerlegen. Den ersten Bruch kürzen. Beim Grenzübergang wird die große Wurzel 1, der erste Bruch also x und der zweite 0.

---

Ich kann es nicht fassen. Es ist so einfach und erst wenn man mich wirklich mit der nase davorstößt kapier ich es.

Answer 1

Hier jetzt eine zusammenfassende Lösung:

$$ \frac { x \cdot \sqrt { 2 n } } { \sqrt { 2 n - x \cdot \sqrt { 2 n } } } \\ = \frac { x \cdot \sqrt { 2 n } } { \sqrt { 2 n - 2 n \cdot \frac{x}{\sqrt{2n}} } } \\ = \frac { x \cdot \sqrt { 2 n } } { \sqrt { 2 n \cdot \left( 1 - \frac { x } { \sqrt { 2 n } } \right) } } \\ = \frac { x \cdot \sqrt { 2 n } } { \sqrt { 2 n } \cdot \sqrt { 1 - \frac { x } { \sqrt { 2 n } } } } $$

$$ \lim _ { n \rightarrow \infty } \frac { x } { \sqrt { 1 - \frac { x } { \sqrt { 2n } } \} 0 } } \\ \frac { x } { \sqrt { 1 } } = x $$

Die Lösung stammt von einem der Kommentatoren. Es ist allerdings ziemlich viel Umformerei von Nöten (muss man erstmal drauf kommen).

Meine Lösung ( bei den Kommentaren ) dürfte mathematisch auch korrekt sein.

Comments

Mein Tipp wäre das Sandwichtheorem, aber die Gauß-Klammern sind echt ein Problem - Ich weiß nicht, wie abschätzen, damit die rausfliegen.

Das war der Fahrplan in der Eingangsfrage: Gaußklammern durch Abschätzen beseitigen.
Für die obere Gaußklammer gilt z ≤ ⌈z⌉ ≤ z+1.

Desweiteren werden beim Grenzübergang Zähler und Nenner unendlich groß, es ist daher eine gute Idee, den dafür haupsächlich verantwortlichen Faktor zu identifizieren und - falls möglich - z. B. wegzukürzen oder sonst wie zu beseitigen. Dieser Faktor ist hier √(2n). Er steht schon im Zähler und kann im Nenner herausgehoben werden. Nach dem Kürzen sehen wir, dass durch den Grenzübergang beide Schranken nun zu x werden.