Ein Trapez durch eine Strecke in zwei inhaltsgleiche Teile zerlegen?

Question

folgende Aufgabe "zerbricht" mir seit gestern den Kopf:

Ein trapezförmiges Grundstück mit a = 51m, b =  75m, α = 90° und β =  110° soll durch eine Strecke PQ in zwei flächeninhaltsgleiche Teile zerlegt werden, wobei P auf der Seite BC 35m von B entfern und Q auf der Seite AD liegt.

Berechne die Entfernung von Q und A!

Irgend ein Tipp mit welchen Rechenschritten ich das berechnen kann?

Comments

Eine Skizze mit ausführlicher Beschriftung ist unerlässlich.

Answer 1

Mache dir zunächst eine Skizze.

Schau dir dann meinen Ansatz an und probiere ihn zu verstehen. Wenn ich Fehler im Ansatz habe korrigiere sie. Dann rechnest du h aus, was der Abstand AQ sein soll.

Ansatz

1/2·51·35·SIN(110°) + 1/2·h·(51 + 35·SIN(20°)) = 1/2·1/2·(51 + 51 + 75·SIN(20°))·75·COS(20°)

Ich komme beim Lösen auf

h = 44.80 m

Comments

 

Das Resultat ist korrekt. Aber ich verstehe die Gleichung nicht ganz. Stellst du hier zwei Flächeninhaltsformen gleich und leitest daraus h (= AQ) ab?

---

Genau. Ich setze die Summe zweier Dreiecksflächen gleich der halben Trapezfläche. Vergleiche die Skizze von mathef. Der hat alle nötigen Hilfslinien eingezeichnet. Eigentlich solltest du diese Aufgabe übernehmen, daher hatte ich meine Skizze extra nicht hier hochgeladen. Aber da die von mathef jetzt schonmal da ist brauchst du ja nur noch meine Formel versuchen zu verstehen. Das Bild dazu hast du.

Answer 2

sieht wohl so aus:

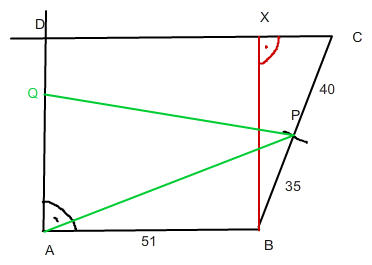
Erst mal die rote Höhe ausrechnen:

h / 75 = sin(70°)

h = 75*sin(70°) = 70,48

Die Strecke s= XC ist dann   s / 75 = cos(70°) gibt s = 25,65

Also die Trapezfläche =  ( 51 + 51+ 25,65) * 70,48  / 2  =  4498,39

Also die Hälfte 2249,19

Das Dreieck ABC hat die Fläche 51*35*sin(110°) / 2 = 838,68

Also muss das Dreieck APQ die Fläche 2249,19 - 838,68 = 1410,51 haben.

Jetzt braucht man noch die Höhe h2 im Dreieck APQ bei P haben.

Dazu vielleicht AP ausrechnen und die beiden Teile von alpha

AP mit cos-Satz im Dreieck ABC 

AP^2 = 51^2 + 35^2 - 2*51*35*cos(110°) = 5047,01

AP =71,04

also sin(alpha1) / sin(110°) = 35 / 71,04 also alpha1 = 27,6°

Und damit alpha2 = 90° - 27,6° = 62,4°

und endlich  h2 / AP = sin(62,4° )

h2 = AP * sin(62,4° ) = 63

Und weil Fläche von APQ = 1410,51 =  0,5 * AQ * h2 = 0,5 * AQ * 63

               1410,51 =  0,5 * AQ * 63

                44,76 = AQ

Comments

Das Dreieck ABC hat die Fläche 51*35*sin(110°) / 2 = 838,68  --> Meinst du hier das Dreieck ABP?

---

genau, war vertippt.