Ganzrationale Funktion mit Achsenschnittstellen x1 = -3, x2 = -1, x3 = 2, y = -3 bestimmen

Question

welche gleichung hat die ganzrationale funktion f, deren graph die x- und die y-achse bei den folgenden koordinaten schneidet?

x1  = -3

x2 = -1

x3 = 2

y = -3

Comments

Die Aufgabe ist nicht sinnvoll formuliert.

---

welche gleichung hat die ganzrationale funktion f, deren graph die x- und die y-achse bei den folgenden koordinaten schneidet?


x1 = -3

x2 = -1

x3 = 2

y = -3

---

Die Aufgabe ist nicht sinnvoll formuliert.

Hm... das nehme ich wieder zurück, die Aufgabe ist schon sinnvoll formuliert. Ich würde die Suche auf eine ganzrationale Funktion dritten Grades beschränken und schlage als Ansatz vor:

f(x) = a*(x-x1)*(x-x2)*(x-x3)

---

das dachte ich auch

dann würde folgendes rauskommen:

a(x+3)(x+1)(x-2)=0


a-6= -3

a= 0,5


lösung:

f(x)= 1/2(x+3)(x+1)(x-2)

---

Ja, das ist richtig.

 

a-6= -3 muss natürlich a*(-6) = -3 heißen.

Answer 1

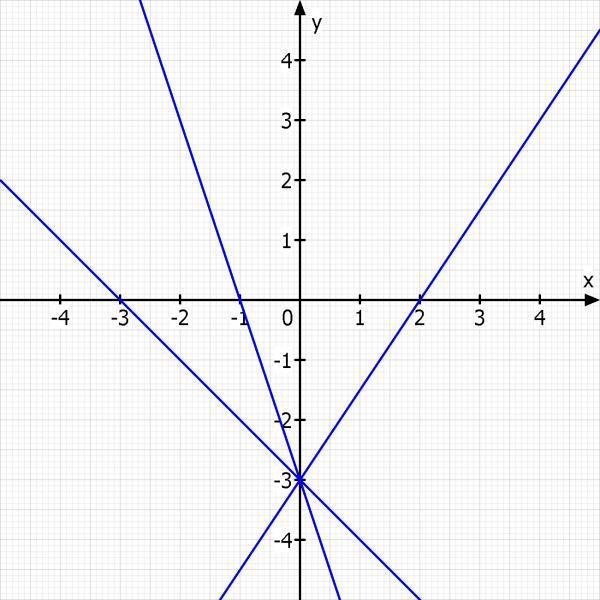
welche gleichung hat f(X), wenn deren graph die x achse und die y achse bei folgenden koordinaten schneidet:

x1 = -3
x2 = -1
x3 = 2

y = -3

f1(x) = -(-3)/(-3) * x + (-3) = -x - 3
f2(x) = -(-3)/(-1) * x + (-3) = -3x - 3
f3(x) = -(-3)/(2) * x + (-3) = 1.5x - 3

Ich habe das mal als 3 Aufgaben interpretiert.