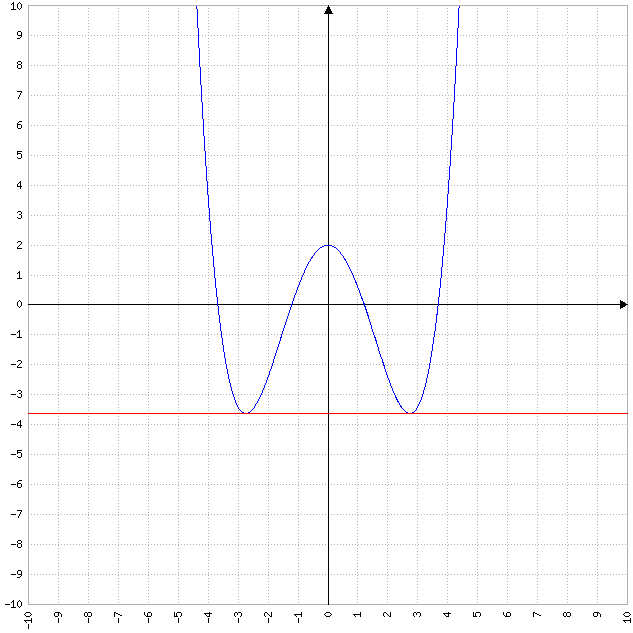
f(x)= 0,4x^4-1,5x^2+2
Ich soll den Flächeninhalt zwischen der Verbindungsgeraden der Minima und f(x) bestimmen.
Habe jetzt die Funktionen subtrahiert und erhalte
0,1+^4-1,5x^2+5,625
Jetzt habe ich einfach die Grenzen genommen, wo die Minima liegen, also ca. 2,7 und -2,7 und integriert. Habe einen Wert von 5,58 raus...stimmt das?