Bestimmen sie den Funktionsterm

Question

Das Schaubild einer Funktion 4. Grades berührt die x-Achse im Ursprung und schneidet die x-Achse in N1(-2/0)

und N2(1/0). Der Punkt P2(2/3) liegt auf Dem Schaubild.

Answer 1

Das Schaubild einer Funktion 4. Grades
berührt die x-Achse im Ursprung und
schneidet die x-Achse in N1(-2/0) und N2(1/0).
Der Punkt P2(2/3) liegt auf dem Schaubild.

Die vielen Nullstellen legen den Ansatz$$ y=a\cdot x^2\cdot(x+2)\cdot(x-1) $$nahe. Die letzte Bedingung legt den noch fehlenden Parameter \(a\) fest und wir erhalten

$$ y = \frac { 3 } { 16 } \cdot x^2\cdot(x+2)\cdot(x-1) $$als Lösung. Ich sehe keinen Grund, warum man das anders machen sollte.

Comments

Ich sehe keinen Grund, warum man das anders machen sollte.
Besser
Ich sehe keinen Grund, warum ich ( az0815 ) das anders machen sollte.

Rasch und elegant gelöst. Sicherlich als Lösungsmöglichkeit wert hier
eingestellt zu werden.

Ob der Fragesteller es versteht ?

Answer 2

Die Bedingungen

f(0) = 0

f'(0) = 0

f(-2) = 0

f(1) = 0

f(2) = 3

Die Gleichungen

e = 0

d = 0

16a - 8b + 4c - 2d + e = 0

a + b + c + d + e = 0

16a + 8b + 4c + 2d + e = 3

Die Lösung des Gleichungssystems

f(x) = 0,1875·x^4 + 0,1875·x^3 - 0,375·x^2

Für ähnliche Aufgaben

http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Answer 3

f(x) = ax⁴ + bx³ + cx² + dx + e

f '(x) = 4ax³ + 3bx² ++ 2cx +  d

f(0) = 0 → e = 0

f '(0) = 0 → d = 0

f(x) = ax⁴ + bx³ + cx² 

f(-2) = 0   →  16·a - 8·b + 4·c = 0

f(1) = 0    →    a + b + c = 0

f(2) = 3    →  16·a + 8·b + 4·c = 3

Die Lösung des LGS ist   a = 3/16 ∧ b = 3/16 ∧ c = - 3/8

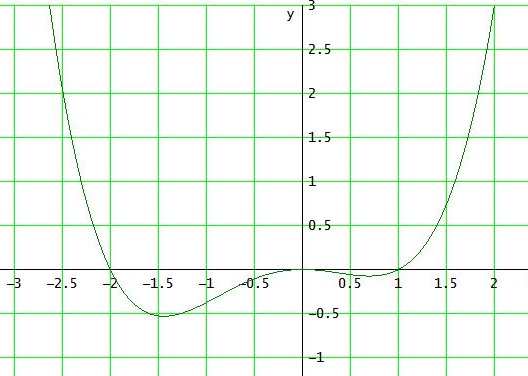
f(x) = 3/16 x⁴ + 3/16 x³ - 3/8 x² 

Gruß Wolfgang