Topologie von Mengen im R^n

Question

ich habe eine kleine Frage zur Topologie im R^n und zwar habe ich folgende Aufgabe:

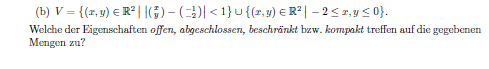
- Das skizzieren ist ja kein Problem, dass ist ein Einheitskeis (ohne Rand ) mit dem Mittelpunkt in (-1|-2) vereinigt mit dem Bereich zwischen der x-Achse und der waagerechten duch -2 (mit dem oberen und unterem Rand

Meine Frage ist jetzt zur Topologie : also ,

-abgeschlossen ist sie nicht , da der Rand vom unteren Einheitskreis nicht in M ist

-offen würde ich sagen ist sie auch nicht, da die werte z.B von der X-Achse in M sind

-beschränkt ist sie glaube ich auch nicht, weil M ja nach links und rechts offen ist

-Kompakt weiß ich nicht genau (nach Heine Borel ja nicht) aber was die Konvergenten Folgen angeht bin ich mir nicht sicher

Wäre cool wenn einer eine Idee hat :)

Comments

Axhso , ja das mit dem Komma in der mit hab ich falsch gedeutet . Danke für die Hilfe

Answer 1

Das skizzieren ist ja kein Problem, dass ist ein Einheitskeis (ohne Rand ) mit dem Mittelpunkt in (-1|-2) vereinigt mit dem Bereich zwischen der x-Achse und der waagerechten duch -2 (mit dem oberen und unterem Rand

Es hieß doch x≥-2  also der Bereich rechts von der Geraden x=-2,

das ist eine parallel zur y-Achse.

Und y≤0 heißt 3. oder 4. Qudrant.

Ich hab das Gefühl der Kreis liegt ganz da drin, also doch abgeschlossen

Die anderen Eigenschaften nicht.