Ist s eine Splinefunktion der Ordnung 3 zur Zerlegung {0, 1.5, 3}?

Question

ich soll zeigen, dass s eine Splinefunktion der Ordnung 3 zur Zerlegung Δ = {0, 1.5, 3} ist.

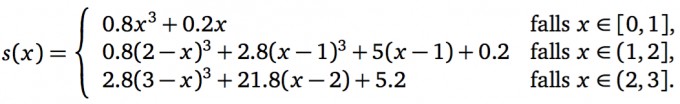
Das einzige Kriterium welches mir noch zu zeigen fehlt:

"Funktion s stimmt auf jedem Intervall [Δ_i, Δ_i+1] mit einem Polynom s_j überein."

Wie zeige ich es am besten? In der Lösung wird gezeigt, dass die dritte Ableitung von s in x = 1 nicht stetig differenzierbar ist und es somit kein Polynom p gibt, sodass s mit p in [0, 1.5] übereinstimmt. Leider verstehe ich es nicht warum es anhand der dritten Ableitung gezeigt wird und wie ich auf den Lösungsweg kommen soll.

,

Robin

Answer 1

Ein anständiger Spline sollte auch die Krümmung und den Ruck an den Übergangsstellen berücksichtigen - und das tut der oben erwähnte gar nicht !!!

Den Ruck zeigt die 3. Ableitung; wird das nicht berücksichtigt, kommt es beim Durchfahren zu einem "Ruck".

Comments

Ruck'n Roll :)