Nullstellen von trigonometrischen Funktionen. sin(2x)+2*cos^2(x)=2

Question

Ich brauche Hilfe bei den folgenden Aufgaben:

a).  Sin(2x)+2*cos²(x)=2

b). 2sin²(x/2)+cos(2x)=1

c). cos²(x)*cos(2x)+1/4cos(2x)=0

Ich komme einfach nicht weiter!

EDIT: Korrigierte Gleichungen aus Kommentaren eingefügt und entsprechende Kommentare entfernt.

Answer 1

Zu Aufgabe a)

Fals diese so lautet:

sin(2x) + 2 cos^2(x)= 2

Es gilt allgemein:

sin(2x) = 2 sin(x) *cos(x)

---------->

2 sin(x) *cos(x) +  2 cos^2(x)= 2 |:2

 sin(x) *cos(x) +   cos^2(x)= 1

cos^2(x) +sin^2(x)=1 allgemein

cos^2(x) =1 - sin^2(x)

sin(x) cos(x) +1 -sin^2(x)=1 |-1

sin(x) cos(x)  -sin^2(x)=0

sin(x)(cos(x) -sin(x))=0

Satz vom Nullprodukt:

1.) sin(x)=0 ----->x_1 = k*π ; k∈ Z

2,) cos(x) -sin(x)=0 | -cos(x)

-sin(x)= -cos(x) |*(-1)

sin(x)=cos(x) | :cos(x)

tan(x)=1 → x_2 = π/4 +k*π ,k∈ Z

-------------------------------------------------------------------------------------------

Zu Aufgabe b)

siehe Anhang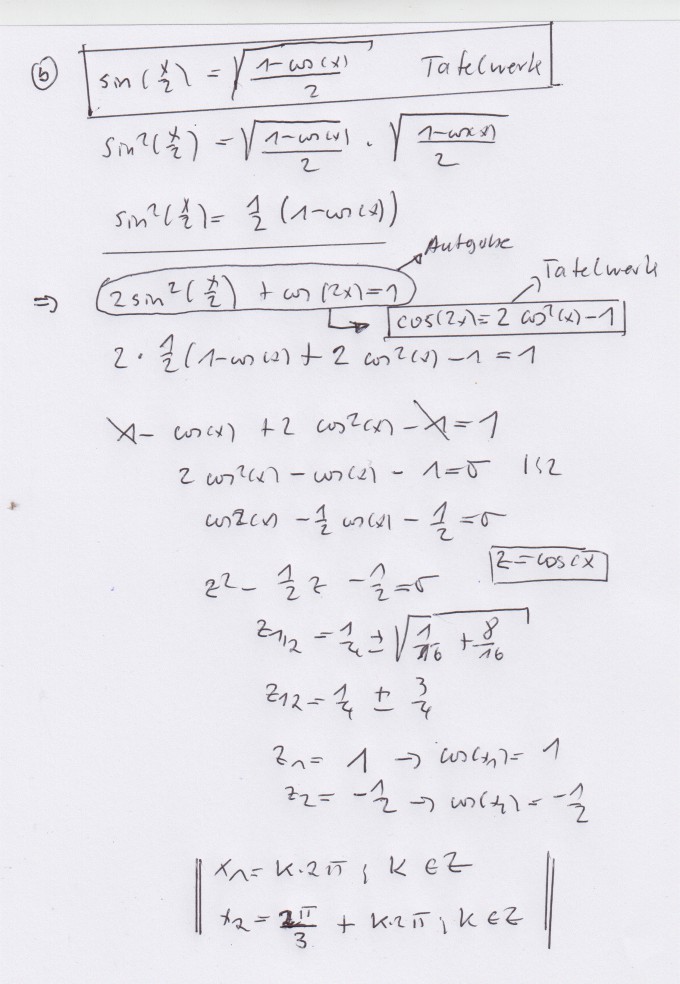

Zu Aufgabe c)

cox(2x) ausklammern

------>

cos(2x) ( cos^2(x) +1/4)=0

-------->Satz vom Nullprodukt:

1.) cos(2x)=0

2.) cos^2(x) +1/4=0

Comments

Danke sehr bis hierhin war ich auch gekommen, aber bei sinx+cosx=2 wusste ich nicht mehr weiter vorzugehen

---

                       
siehe oben

---

Vielen vielen Dank du warst eine super Hilfe, danke nochmal für die Mühe!