Ableitung; Differenzenquotient etc.

Question

Hallo :D, ich wollte fragen ob mir jemand einmal die lokale und die mittlere änderungsrate erklären könnte und einmal die Funktion der Tangente und der Sekante, weil ich das vom Internet einfach nicht verstehe. 

Vielen dank schonmal! 

Answer 1

Momentane Änderungsrate f'(x) 

Mittlerer Änderungsrate im Intervall [a, b] = (f(b) - f(a)) / (b - a)

Tangentengleichung an einer Stelle a: y = f'(a) * (x - a) + f(a)

Sekante an den Stellen a und b: y = (f(b) - f(a)) / (b - a) * (x - a) + f(a)

Answer 2

Hallo :D, ich wollte fragen ob mir jemand einmal die lokale
und die mittlere änderungsrate erklären könnte und einmal die
Funktion der Tangente und der Sekante, weil ich das vom
Internet einfach nicht verstehe.

Die mittlere Änderungsrate wird zwischen 2 Punkten ermittelt.
siehe die 1.Skizze
P ( x | y )
P2 ( 5 | 500 )
P1 ( 2 | 300 )

m = Δ y / Δ x = ( y2 - y1 ) / ( x2 - x1 ) = ( 500 - 300 ) / ( 5 - 2 )
m = 66.66
Pro eine x-Einheit ändert sich y um 66.66

Dies ist der Differenzenquotient oder mittlere Änderungsrate.

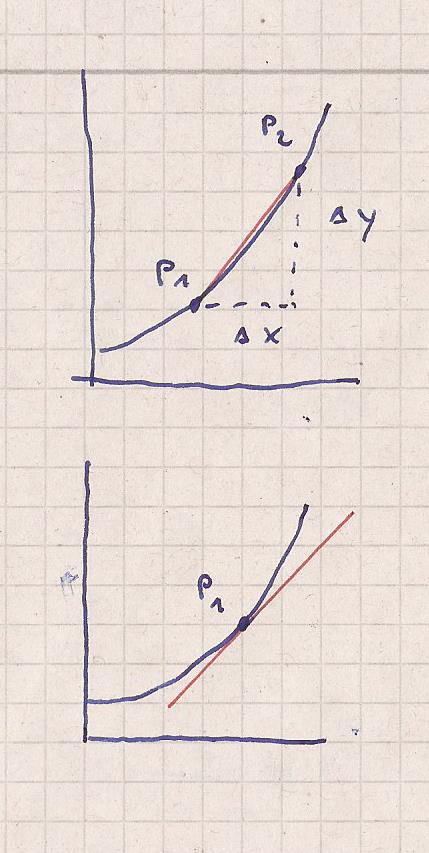
Läßt man nun P2 gegen P1 gehen wandelt sich die mittlere Änderungsrate
in die lokale ( örtlliche ) Änderungsrate im Punkt P1.
Dies ist die Steigung der Kurve im Punkt P1.
siehe Skizze 2

Aus dem Differenzenquotient wird der Differntialquotient.
Der Differentialquotient kann z.B. mit der h Methode berechnet werden
und entspricht der 1.Ableitung der Differentialrechnung.

Beide Geraden haben eine Funktionsgleichung
y = m * x + b
m ist bereits bekannt

- 1.Fall Sekante
y(P2) = m *x ( P2 ) + b
500 = 66.66 * 5 + b
b = 166.66
y = 66.66 * x + 166.66

- 2.Fall Tangente
y ( P1 ) = m ( P1 ) * x ( P1 )  + b