f(x) = (x^4 - 8x^2 + 16) / (2x^2)
f'(x) = (x^4 - 16) / x^3
f''(x) = (x^4 + 48) / x^4
Definitionsmenge
Ich darf für x alles einsetzen außer Null, weil man durch Null nicht teilen darf. D = R \ {0}
Symmetrie
Wir haben nur gerade Potenzen von x und somit eine Achsensymmetrische Funktion
Y-Achsenabschnitt f(0)
Nicht Definiert
Nullstellen f(x) = 0
x^4 - 8x^2 + 16 = 0
z^2 - 8z + 16 = 0
z = 4
x = ± 2
Definitionslücken. Art und Verhalten an den Definitionslücken
x = 0
lim x→0- f(x) = ∞
lim x→0+ f(x) = ∞
Extrema f'(x) = 0
x^4 - 16 = 0
x = ± 2
Die Nullstellen sind gleichzeitig Extrema. Und da die Funktion gegen 0 ins unendliche Wächst sind das zwei Tiefpunkte.
Monotonieverhalten
Monoton steigend für x [-2, 0[ und [2, ∞[
Monoton fallend für x ]-∞, -2] und ]0, 2[
Wendestellen f''(x) = 0
x^4 + 48 = 0
Kann nicht null werden, daher keine Krümmung. Die Funktion ist an jeder Stelle linksgekrümmt.
Grenzverhalten
lim x→-∞ f(x) = ∞
lim x→∞ f(x) = ∞
Asymptotik
Die y-Achse ist vertikale Asymptote
Polynomdivision
(x^4 - 8x^2 + 16) / (2x^2) = 1/2x^2 - 4 + 8/(x^2)
Eine Asymptote ist 1/2*x^2 - 4
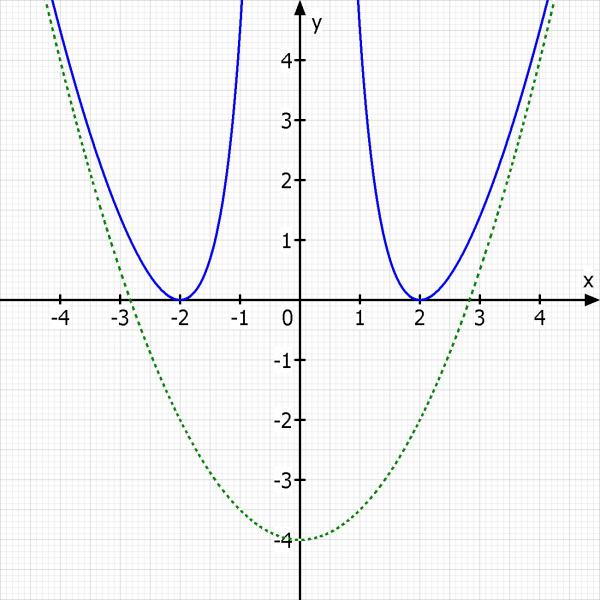
Skizze der Funktion