Die zeitliche Entwicklung eines Pilzbefalls nach Anwendung eines Pilzbekämpfungswirkstoffes lässt sich durch die Differentialgleichung
Ṗ(t) = (-2*t/ (1+t2) + cos t) P(t)
beschreiben; dabei bezeichnet t -> P(t) die Stärke des Befalls zur Zeit t >= 0 (in Monaten).
(i) Bestimmen Sie die Lösung der Differentialgleichung für t 0 zur Anfangsmasse P(0) = P0.
Lösung der Differenzialgleichung siehe
https://www.wolframalpha.com/input/?i=dy%2Fdt+%3D+%28-2*t%2F%281%2Bt%5E2%29+%2B+cos%28t%29%29+*+y
P(t) = c·e^SIN(t)/(t^2 + 1)
P(0) = c = P0
P(t) = P0·e^SIN(t)/(t^2 + 1)
(ii) Wie verhält sich der Pilzbefall gleich nach dem Beginn der Behandlung? Und was ist das langfristige Verhalten des Pilzbefalls, also für t -> unendlich ?
Ṗ(0) = P0
Damit haben wir im Zeitpunkt 0 quasi eine Verdopplungsrate.
lim t-->∞ P(t) = 0
Langfristig geht der Befall aber auf 0 zurück.
(iii) Angenommen die Behandlung mit dem Wirkstoff beginnt am 15. Juli. Kann man dann ausschließen, dass die Stärke des Pilzbefalls nach dem 15. Oktober noch einmal größer werden wird als die Hälfte des Anfangswertes P0 (mit Begründung; eine grobe Abschätzung reicht aus) ?
P(t) = c·e^SIN(t)/(t^2 + 1)
Wenn wir für t = 3 einsetzen dann ist der Nenner 10. Damit müsste e^sin(t) aber 5 werden. Das geht nicht. sin(t) kann höchstens 1 werden und e^1 ist maximal 2.718.
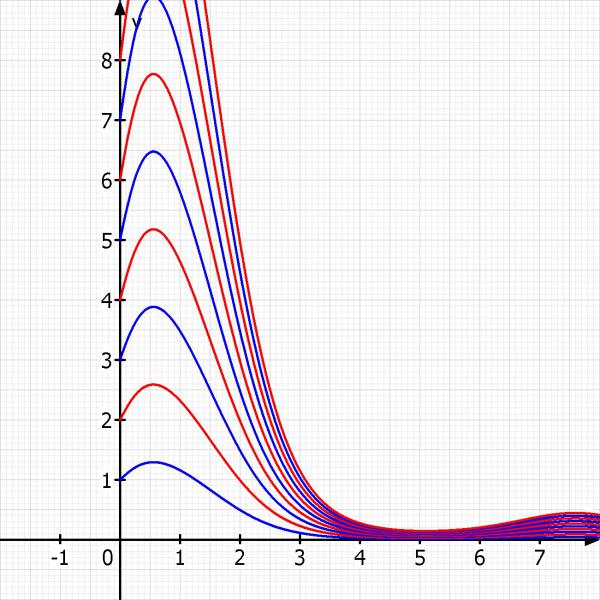
Skizze