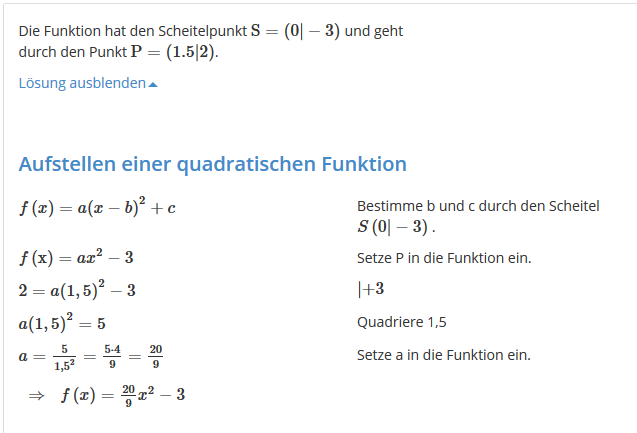
Die Aufgabe: Die Funktion hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(1,5|2). Stellen Sie die Funktionsgleichung auf (Scheitelform und allgemeine Form).
Ich habe so gerechnet:
f(x)=a(x-d)2+e ist ja die Scheitelpunktform, also einfach den Scheitelpunkt einsetzen und man bekommt f(x)=a(x-0)2-3
Dann hab ich P in die Scheitelpunktform gesetzt, also a(1,5-0)2-3=2 und dann nach a aufgelöst.
Detailliert:
a(1,5-0)2-3=2
2,25a-3=2 |+3
2,25a=5 |:2.25
Bei mir kam raus a=2.
Die Scheitelpunktform wäre demzufolge f(x)=2(x-0)2-3 und die Normalform f(x)=2x2-3.
Allerdings steht bei der Lösung der Aufgabe was ganz anderes als mein Ergebnis und ich frage mich, ob und wo ich einen Fehler gemacht habe. Der Screenshot der anderen Lösung ist unten. Kann mir bitte jemand erklären, wie die Person, die die Lösung aufgestellt hat, da jetzt auf a=20/9 kommt?!?
Danke für alle Antworten.
Mfg
Nora