Ein Baumdiagramm veranschaulicht das:
[ #E in meinem "Vordruck" spielt hier keine Rolle :-) ]
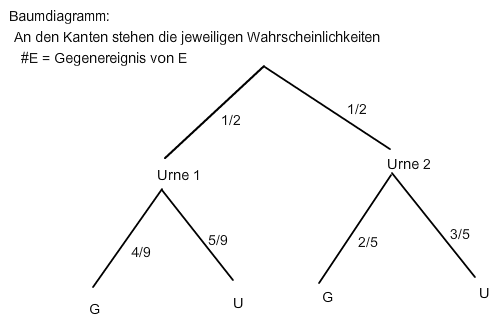
Sei U1 = "gezogene Kugel stammt aus Urne1" , G = "gezogene Kugelnummer ist gerade"
PG(U1) = P(U1) unter der Bedingung G [ hier gesucht! ]
PG(U1) =Def. P(U1 ∩ G) / P(G) = ( 1/2 * 4/9) / ( 1/2 * 4/9 + 1/2 * 2/5 ) = 10/19
Gruß Wolfgang