Warum ist der Sinus nicht um π/2 verschoben?

Question

a := sin(2x+(π/2))
b:= sin(2(x+(π/2)))

mir erschließt sich nicht, wieso a die Sinus-Kurve nicht um π/2 verschiebt, 
aber b es wirklich tut. 

 

Comments

Überleg mal, wo z.B. jeweils die erste Nullstelle vom Sinus landet. (Du weißt ja sicher, dass sin(0) = 0 ist.)

---

Das Gegenteil ist der Fall :

a.   verschiebt die Sinus-Kurve um pi/2.

---

> a.   verschiebt die Sinus-Kurve um pi/2. 

Ich denke nicht, dass hier überhaupt die "Sinuskurve" verschoben wird, sondern der Graph von sin(2x)

Bei a) beträgt die Phasenverschiebung  - π/2 , nicht die Verschiebung der Kurve

---

Ich denke nicht, dass hier überhaupt die "Sinuskurve" verschoben wird

Bei a. doch.

Mit "die Sinuskurve" ist ja wohl der Graph der Funktion f mit  f(x) = sin x  gemeint.
Dieser Graph wird bei a. um pi/2 (nach links) verschoben, anschließend wird der so verschobene Graph mit dem Faktor 2 in x-Richtung gestaucht.
Bei b. ist die Reihenfolge der Transformationen vertauscht.

---

Dann präzisieren wir das:

Die Aussage:

"Der Graph von f_a  ergibt aus dem der Funktion f(x) = sin(x) [Sinuskurve] durch eine Verschiebung von f um π/2" 

ist falsch.

Und deine "Aussage"    "> a.   verschiebt die Sinus-Kurve um pi/2."   wird wohl jeder unvoreingenommene Leser  so interpretieren.

[ Vielleicht solltest du bei solchen Kommentaren den Entschlüsselungscode mitliefern ]

Answer 1

Hi,

die allgemeine Form eines Sinus sieht so aus:

y = a*sin(b(x+c)) + d

Wenn Du eine Verschiebung bewirken willst, musst Du also den Faktor b berücksichtigen.

Grüße

Answer 2

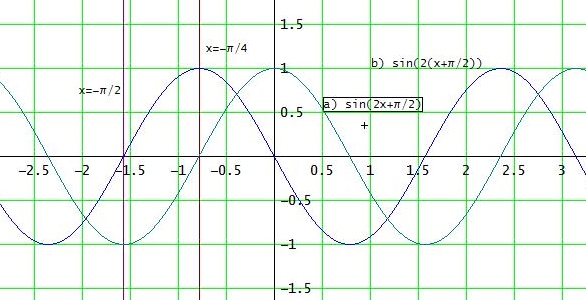
Bei b) wird der Graph von sin(2x)   um π/2 nach links (oder rechts) verschoben 

   Die Sinuskurve sin(x)  wird dabei in x-Richtung mit dem Faktor 1/2 gestreckt und dann       um π/2 verschoben.

   Die sogenannte "Phasenverschiebung" beträgt -π (oder π)

Bei a) wird der Graph von sin(2x)   um  π/4  nach links verschoben.

Die Sinuskurve sin(x)  wird dabei in x-Richtung mit dem Faktor 1/2 gestreckt (die Periode wird also halbiert) und dann um π/4 nach links verschoben.

      Die "Phasenverschiebung" beträgt  -π/2

[ Die Phasenverschiebung ergibt sich jeweils aus dem Vergleich mit  f(x) = sin(x): 

  Der 1. Hochpunkt  wird zum Beispiel bei b) um π/4  nach links (- π/4) auf die y-Achse          verschoben. 

   Bei f(x) = sin(x) entspricht das einer Verschiebung um - π/2 ]

Gruß Wolfgang

Answer 3

a := sin(2x+(π/2))
b:= sin(2(x+(π/2)))

mir erschließt sich nicht, wieso a die Sinus-Kurve nicht um π/2 verschiebt, 
aber b es wirklich tut.

Hallo jb4133,

deine Frage ist meiner Meinung nach nicht ganz präzise formuliert.
Ich  vermute du meinst den Sachverhalt

Grundfunktion
f ( x ) = sin ( 2 * x )

a ( x ) = sin ( 2 * x + π/2 )
b ( x ) = sin ( 2 * ( x + π/2 ) )

b kann ausmultipliziert werden und es ergibt sich

f ( x ) = sin ( 2 * x )

a ( x ) = sin ( 2 * x + π/2 )
b ( x ) = sin ( 2 * x + π )

a und b sind demnach beide Verschiebungen von f.

mfg Georg

Comments

Das ist doch gerade falsch herum.

a ist deshalb eine Verschiebung von f, weil man den Faktor 2 ausklammern kann.
Man erhält  a(x) = sin ( 2*(x + π/4) ) .  Es handelt sich also um eine Verschiebung von (deinem) f um π/4 .

---

Hallo jb4133,

so langsam dämmert es mir was du hast fragen wollen
bzw. was dein Problem ist.

Du willst eine x-beliebige Funktion um ein bestimmtes Maß in Richtung
x-Achse verschieben. In deinem Beispiel ist
a.) ist nicht richtig
b.) ist richtig.
Warum ?

Ich gehe die Sache allgemeingültig an :
Du hast eine Funktion z.B.
f ( x ) = x^2
f ( 0  ) = 0^2 = 0
und suchst eine neue Funktion bei der diese Funktion um 1 nach rechts
verschoben wird. Dafür gilt
b ( 1 ) = f ( 0 ) = 0
b ( 1 ) = f ( 1 - 1 ) = 0
allgemein
b ( x ) = f ( x -1 )
f ( x -1 ) = ( x - 1 ) ^2
b ( x ) = ( x -1 )^2

weiteres Beispiel
f ( x ) = x^2 + x * √ x
soll um 2 Einheiten nach links verschoben werden
f ( x +2 ) = ( x+2 )^2 + ( x +2 ) * √ ( x +2 )
b ( x ) =  ( x+2 )^2 + ( x +2 ) * √ ( x +2 )

Du mußt also überall wo in der Originalfunktion das " x " steht dies durch
" x +2 " ersetzen.

In deinem Beispiel
f ( x ) = sin ( 2 * x )
wird zu ( Verschiebungswert + π/2 )
f ( x + π/2 ) = sin [ 2 * ( x + π/2 ) ]
b ( x ) =  sin [ 2 * ( x + π/2 ) ]

mfg Georg