a.) 1+2+3+...+(n-1)+n=?
Du suchst die blaue Fläche:
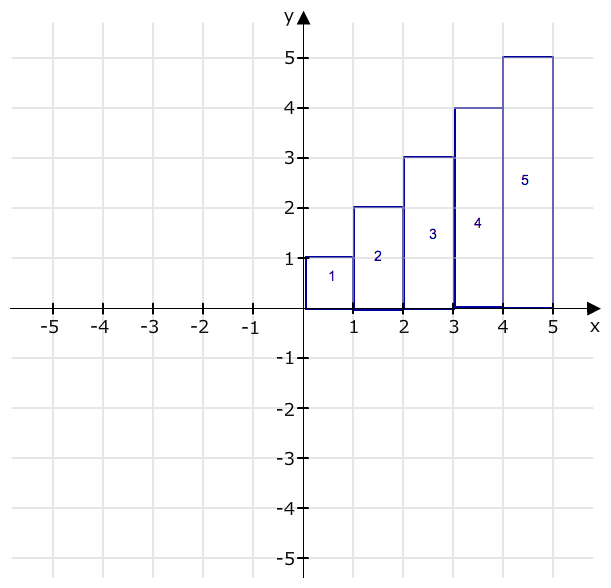
Und kannst das geometrisch so anschauen:
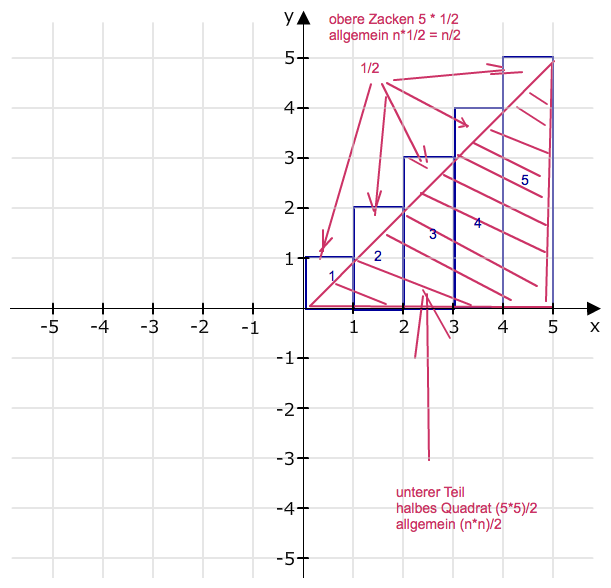
1+2+3+...+(n-1)+n= n/2 + n^2/2 = (n + n^2)/2 = (n*(n+1))/2
Bei b) und c) kannst du auch geometrisch vorgehen.
b.) 1+3+5+...+(2n-3)+(2n-1)=?
c.) 2+4+6+...+2(n-1)+2n=?