Zeichne in der komplexen Ebene mit bestimmten Voraussetzungen

Question

SO letzte Frage für heute!! sorry aber ich bin mir dabei so unsicher.

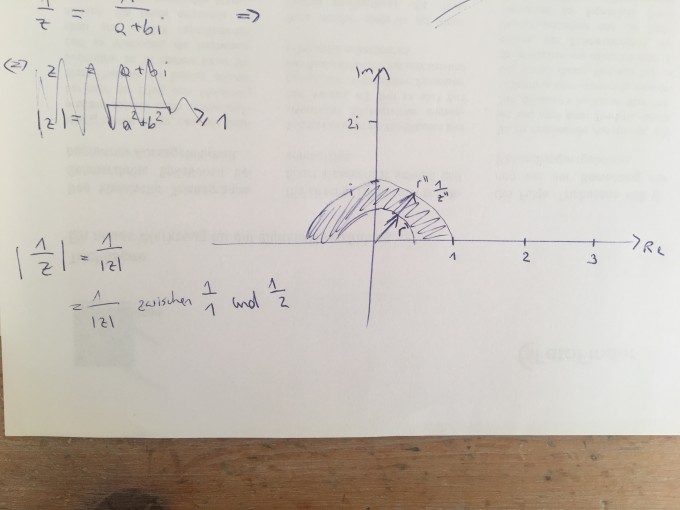
folgendes ist gegeben nämlich man soll die Menge aller 1/z zeichnen wobei 1 <= |z| < 2 gilt und Im(z)> 0

1/z ist doch eigentlich eine Stauchung des radius von 1/z oder? 

ich habe es so interpretiert, stimmt das?

Answer 1

Ich wuerde mich an die Formel $$\frac{1}{z}=\frac{\overline{z}}{|z|^2}$$ halten.

Comments

also is das obere total falsch?

Ich dachte |1/z| ist dann die Strecke von 1/z  zu (0;0).

Ich versteh gar nix mehr o.O

---

Sicher ist \(|1/z|=1/|z|\). Aber Du brauchst auch noch eine Richtung. Und das ist die von \(\overline{z}\), nicht die von \(z\). Du musst Dein Bild noch an der reellen Achse spiegeln. $$1/z=\underbrace{\overline{z}/|z|}_{\text{Einheitsvektor in Richtung $\overline{z}$}}\cdot\underbrace{1/|z|}_{\text{Betrag von $1/z$}}$$