Quadratische Funktionen und Gleichungen Parabeln

Question

Julia hat ein Bild mit den Seitenlängen 20 cm und 30 cm gemalt ,

das noch von einem Passepartout umgeben werden soll , dass auf allen Seiten gleich breit ist.

Die Kunstlehrerin emphielt für eine gute Wirkung , das Passepartout so groß zu wählen ,

dass es 40 % der gesamtfläche einnimmt.

Wie groß muss das Passepartout gewählt werden .

Comments

Vom Duplikat:

Titel: Quadratische Funktionen/ Gleichungen/ Ergänzungen: Bild soll von einem Passepartout umgeben werden.

Stichworte: quadratische,gleichung,bild,rahmen,passepartout

Kann mir jemand bei der Textaufgabe helfen? 

Julia hat ein Bild mit den Seitenlängen 20cm und 30cm gemalt, das noch von einem Passepartout umgeben werden soll, das auf allen Seiten gleich breit ist. Die Kunstlehrerin empfiehlt für eine gute Wirkung, das Passepartout so groß zu wählen, dass es 40% der Gesamtfläche einnimmt. Wie groß muss das Passepartout gewählt werden?

(Wir hatten noch keine pq-Formel, nur quadratische Ergänzung)

Answer 1

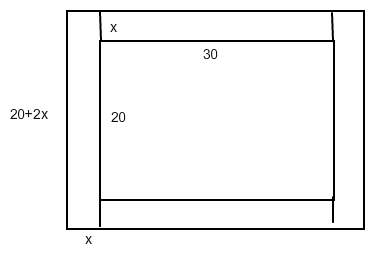
x cm sei die Breite des Rahmens:

2 * [ (20+2x) * x + 30*x ] =  0,4 *  [ 2 * [ (20+2x) * x + 30*x ]  +  20*30 ]

Fläche des Rahmens , Fläche des Bildes

rechts [...]  auflösen:

2 * [ (20+2x) * x + 30*x ] =  0,8 * [ (20+2x) * x + 30*x ]   + 240 

1,2 *  [ (20+2x) * x + 30*x ]  - 240 = 0

Ausmultiplizieren und zusammenfassen:

12/5 ·x²  + 60·x - 240 = 0  | * 5/12

x² + 25·x - 100 = 0

pq-Formel →   x ≈  3.51      [   x₂ ≈  -28.51 < 0   entfällt ] 

> Wie groß muss das Passepartout gewählt werden . 

Er hat dann die Außenmaße  (20+2x) cm  und (30+2x) cm  

Gruß Wolfgang 

Answer 2

Die Fläche des Passepartout soll 40% der Gesamtfläche (Passepartout und Bild) sein, also soll das Bild 60% der Fläche einnehmen. $$20cm\cdot30cm=600cm^2$$ sollen also 60% der gesamten Fläche sein. Wenn 60% 600cm² sind, wieviel cm² sind dann 100%?

Zur quadratischen Gleichung kommen wir jetzt, denn das Bild soll gleichmäßig eingerahmt sein. Also soll $$(20+x)\cdot(30+x)=1000.$$

20+x und 30+x deshalb, weil damit sichergestellt ist, dass der Rand in allen Richtungen gleich weit vom Bild entfernt ist, solange man das Bild zentriert (der Abstand ist dann jeweils x/2).

$$(20+x)\cdot(30+x)=1000\Leftrightarrow 600+50x+x^2=1000\Leftrightarrow x^2+50x-400=0.$$

Versuch mal, von da weg mit quadratischer Ergänzung weiterzurechnen.

Comments

Hi,danke für deine Hilfe, ist es richtig, dass das Bild ohne den Rahmen 20cm*30cm groß ist oder ist das passepartout schon dabei?

---

Ja, das Bild alleine hat das Format 20x30 cm.

---

Okay, danke!

Muss man nicht in den Klammern (20+x)*(30+x)=1000

daraus 

(20+2x)*(30+2x)=1000 machen, weil es kommen doch zweimal x wegen der linken und er rechten seite dazu, oder?

---

Das kommt darauf an, was genau du x nennst. Ich habe mit x die Länge gemeint, die zur Länge (oder alternativ Breite) des Bildes dazukommt. Du hingegen hast mit x den Abstand vom Rand des Bildes zum Rand des Passepartout bezeichnet. Dein x ist einfach halb so groß wie meins. Also ja, wenn du mit deinem x rechnen willst, musst du immer 2x schreiben, wo ich x stehen habe.

Answer 3

Zunächt mal rechnet man aus, wie groß ein Bild werden muss damit 20·30 gerade 60% davon sind. Ein solches Bild hat die Größe 1000 cm². Da der Rand x überall gleich ist, muss gelten (20+x)(30+x)=1000. Diese quadratische Gleichung hat die ungefähre positive Lösung x= 7. Das Bild mit Passepartout misst also 27x37 cm.

Comments

Hi, ich verstehe die selbe Aufgabe nicht.

Wie kommt man auf die 1000cm²?

---

Dreisatz 20·30 =  600 entsprechen 60%

                                 10 entsprechen 1%

                             1000 entsprechen 100%