Verbal Beschreibung dem Verlauf des Graphen der Funktion und evtl ihn zeichnen

Question

Verbal Beschreibung dem Verlauf des Graphen der Funktion und eventuell ihn zeichnen f:f(x)=3+0,2+(x+1)hoch2-4

Comments

Hallo Gloria,

> 3 + 0,2 + (x+1)hoch2 - 4          [ 3 + 0,2 + (x+1)² - 4 ] 

= - 0,8  + (x+1)hoch2

Die Funktionsangabe wäre deshalb sehr ungewöhnlich.

Bist du da sicher?

Gruß Wolfgang

---

Sorry, es sollte 3+0,2 (x+1)hoch2-4 sein. 

---

Habe meine Antwort  diesbezüglich ergänzt

---

Hallo erst einmal. 

Ich versuche mich gerade dabei mein Fachabi zu machen. In der einen Matheaufgabe haben wir genau die gleiche Funktion wie oben genannt. Irgendwie stehe ich auf dem Schlauch , aber ich verstehe die Rechenweise gerade gar nicht. Kann man dies eventuell Stück für Stück ausführlich aufschreiben und erklären? Wäre echt toll.

LG und danke Anja

Answer 1

Hallo Gloria,

> f(x)  =   3 + 0,2*(x+1)hoch2- 4

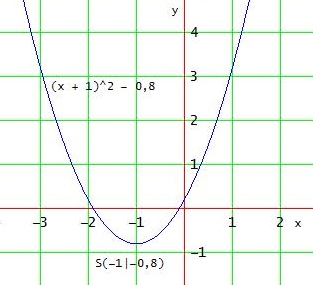
 f(x)  =   (x + 1)² -  0,8

Das ist die Scheitelform einer nach oben geöffneten Normalparabel mit dem Scheitelpunkt  S(-1 | - 0,8)

Sie hat also die Wertemenge [ - 0,8 ; ∞ [  und ist 

streng monoton fallend in  ] - ∞ ; -1 ]   und  streng monoton steigend in [ -1 ; ∞ [ 

Außerdem ist der Graph linksgekrümmt.

Der Grenzwert für x → ± ∞ ist jeweils ∞ .  

Nachtrag mit korrigierter Funktion:

> f(x) = 3+0,2(x+1)hoch2-4

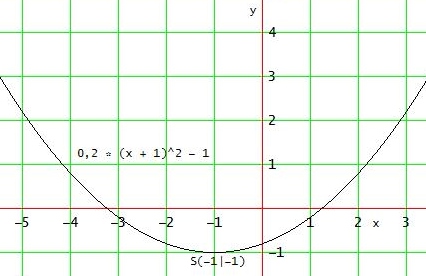
f(x) = 0,2 * (x+1)² - 1        S( -1 | - 1 )

Die Beschreibung kannst du jetzt oben abschreiben, wenn du -0,8 durch -1 ersetzt.

Gruß Wolfgang

Comments

Danke, du hast mich gerettet:)