Hallo Firana,
N1)
| x2 - 4 | / (x+1) > 4
Es muss x+1 > 0 [ #also x > -1 ] gelten, da der Bruch sonst nicht positiv, insbesondere also nicht > 4 sein kann.
x2 - 4 ≥ 0 ⇔ x≥2 oder x ≤ -2 , #also x≥2
1.Fall: x≥2 ( | ...| kann entfallen )
x2 - 4 > 4 * (x+1)
x2 - 4 > 4x + 4
x2 - 4x - 8 > 0
Mit der pq-Formel erhält man die Nullstellen x1 = 2 - 2·√3 und x2 = 2·√3 + 2
des linken Parabelterms (nach oben geöffnete P.)
der Parabelterm ist also für x < 2 - 2·√3 oder x > 2·√3 + 2 positiv
L1 = ] 2·√3 + 2 ; ∞ [
2.Fall: x<2 , #also -1 < x < 2 ( |...| durch Minus vor Klammer ersetzen )
- (x2 - 4) > 4 * (x+1) | * (-1)
x2 - 4 < -4x - 4 ( Multiplikation mit (-1): > → < )
x2 + 4x < 0
x * (x+4) < 0
Der Parabelterm ist für -4 < x < 0 negativ
L2 = ] -1 ; 0 [
L = L2 ∪ L1 = ] -1 ; 0 [ ∪ ] 2·√3 + 2 ; ∞ [
----------------
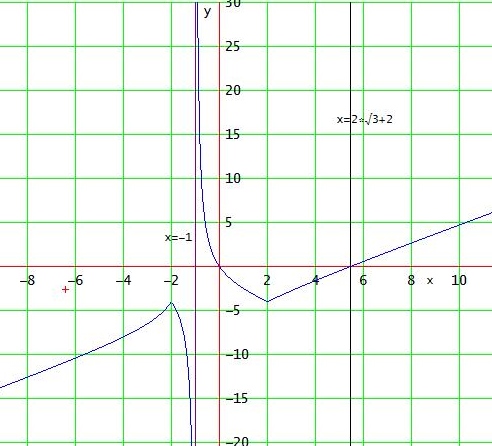
| x2 - 4 | / (x+1) > 4 ⇔ | x2 - 4 | / (x+1) - 4 > 0
Hier der Graph von f(x) = | x2 - 4 | / (x+1) - 4
Gruß Wolfgang