Tangentenabschnitte berechnen

Question

kann mir wer bei dieser Aufgabe helfen! Ich komme nicht weiter

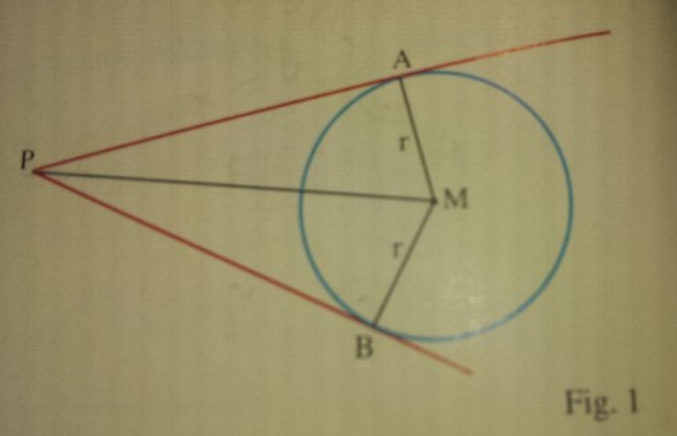
( 13) Von einem Punkt \( P \) werden zwei Tangenten an den Kreis um M mit dem Radius r gezeichnet (Fig. I). Berechne die Tangentenabschnitte \( \overline{\mathrm{PA}} \) und \( \overline{\mathrm{PB}} \) für
a) \( r=4,0 \mathrm{cm}, \quad \overline{\mathrm{MP}}=5,8 \mathrm{cm} \)
b) \( r=9.5\, \mathrm{cm} , \quad  \overline{\mathrm{MP}}=13 \mathrm{cm} \)

 

Answer 1

Rechne bei a) und b)

| PA | = | PB | = √ ( |PM|^2 - r^2)

Begründung: Tangenten an einen Kreis stehen senkrecht auf den zu ihnen gehörigen Radien des Kreises.

Answer 2

zu a) (Ich lasse den Strich und die Einheiten mal jetzt weg)

PM^2 = AP^2 +r^2

PM^2 -r^2= AP^2

AP= ±√(PM^2 -r^2)

AP= 4.2 cm, die negative Lösung entfällt.

PB^2 +r^2= PM^2

PB hat auch als Lösung 4.2 cm.

b) geht analog zu rechnen