Funktionsschar und Graphen

Question

!
Ich komme bei einigen Aufgaben nicht weiter und ich hoffe ihr könnt mir helfen.

Betrachten Sie die Funktionsschar f_b,c = x³ + bx² + cx mit b,c  ∈ ℝ.

a) Geben Sie ein Paar von Werten für b,c so an, dass f_b,c genau eine Nullstelle besitzt.
     Hier habe ich wirklich überhaupt keine Idee! 

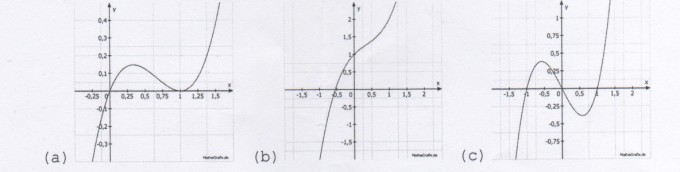
b) Sei nun b = -2, c = 1. Kreuzen Sie an, welche Abbildung den Graphen von f_-2,1 zeigt.
     Meine Lösung: a)     Ist das korrekt? - Siehe Bild - 

c) Geben Sie an, wie b,c gewählt werden müssen, damit der Graph von f_b,c punktsymmetrisch zum Ursprung ist.
     Hier stehe ich wieder auf dem Schlauch. Ich habe keine Idee!

     

Answer 1

Zu a) f(x)= x³+bx²+cx = x(x²+bx+c). Eine Nullstelle ist in jedem Falle x=0. Also darf x²+bx+c=0 keine Lösung haben. Nach der pq-Formel ist x_1/2=-b/2±√(b²/4-c). Wenn der Radikand (b²/4-c) negativ ist, gibt es keine Lösung. Ein Paar von Werten wäre b=2 und c=2. Dann ist √(-1) nicht reell und es gibt nur die oben schon erwähnte Nullstelle x=0-

Comments

Zu c) Wenn b = 0 und c beliebig, dann heißt die Funktionsgleichung f(x) = x³-cx und ist punktsymmetrisch zum Ursprung des Koordinatensystems (nur ungerade Exponenten von x).

---

Vielen Dank für deine Hilfe! :)