Ich könnte mir so was vorstellen.
Du hast eine begrenzte Anzahl von Personen die infiziert werden können, z.B. \( G = 1000 \) und am Anfang sind \( f(0) = 2 \) infiziert. Nach T = 2 Wochen sind aber schon 10 infiziert. Wie ist der Verlauf der Infizierten.
Die logistische Kurve hat ja folgendes Aussehen
$$ f(t) = \frac{G}{1+e^{-k \cdot G \cdot t} \left( \frac{G}{f(0)} - 1 \right) } $$
Hier bei wäre \( G = 1000 \), \( f(0) = 2 \) und \( k \) berechnet sich aus der F´Gleichung
$$ f(2) = \frac{1000}{1+e^{-k \cdot 1000 \cdot 2} \left( \frac{1000}{2} - 1 \right) } = 10 $$,
d.h. \( k = \frac{ \ln \left( \frac{G}{f(0)} \right) - \ln \left( \frac{G}{f(2)} \right) }{T \cdot G} = 0.00081 \)
Dann sieht der Infektionsverlauf so aus
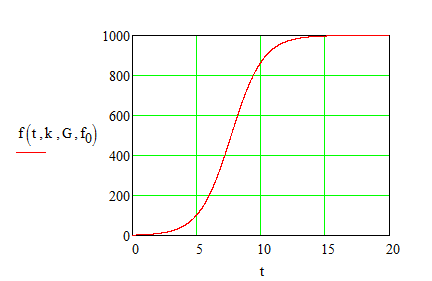
Allerdings gibt es hier keine Gesundungen. Das ist nur mit den anderen Modellen (SI...) wie vorher erwähnt nur möglich.