Auch wenn die "beste Antwort schon vergeben wurde, möchte ich die exakte Lösung zeigen:
Wer die Umkehrfunktion von x*e^x , also LambertW(n,x)
kennt siehe
http://www.lamprechts.de/gerd/LambertW-Beispiele.html
findet sofort die exakte Lösung:
5/100=exp(-x)*(1+x)
e^x=20x+20
§5 mit a=1, b=20, c=20
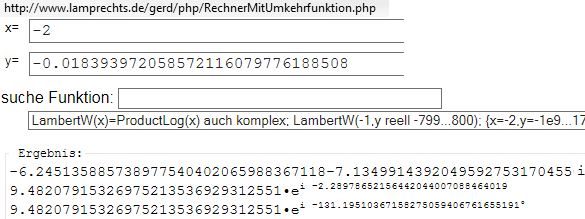
x=-LambertW(n , -a/[b*e^{a*c/b}]) /a - c/b, n=-2...2
x=-LambertW(n, -1/[20*e^{20/20}])-1
x=-LambertW(n, -1/[20*e])-1
x=-LambertW(n,-0.018393972058572116079776188508)-1
n | f(n)..........................................................................
-2 | 5.2451358857389775404020659883628..+7.134991439204959275317045509645.. i
-1 | 4.7438645183905783758502737858333..
0 | -0.981258037995027972440746836896..
1 | 5.2451358857389775404020659883628..-7.134991439204959275317045509645.. i
2 | 5.7197772157006401464677735849881..-13.68059170482760971191352904771.. i
Probe ergibt für alle 5 Lösungen des gesuchte Ergebnis 0.05
Gute Rechner kennen LambertW(reell)
sehr gute Rechner kennen auch noch 2 weitere komplexe Lösungen
( http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php )