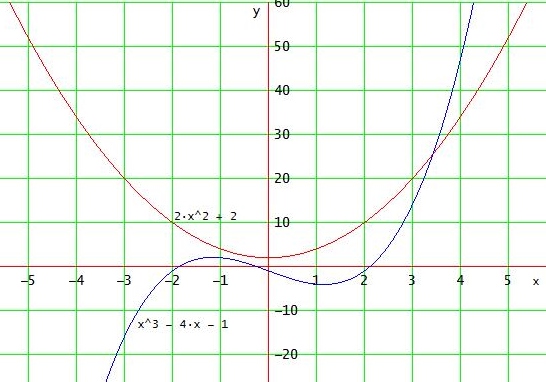
es sollen wohl die x-Werte berechnet werden, an denen die Steigungen gleich sind, denn die Graphen haben zwar einen gemeinsamen Punkt, aber dort sind die Steigungen nicht gleich:
4x = 3x2 - 4 ist richtig
3x2 - 4x - 4 = 0
x2 - 4/3 · x - 4/3 = 0
ax2 + bx + c = 0
abc-Formel: a = 3 , b = - 4 , c = - 4
x1,2 = ( - b ± \(\sqrt[]{b^2-4ac}\)) ) / (2a)
....
x1 = 2 ; x2 = - 2/3
Die parallelen Tangenten mit gleicher Steigung an diesen Stellen lassen sich im Graph wegen der verschiedenen Skalierung der Achsn nicht erkennen.
Gruß Wolfgang