Kann mir jemand helfen
Ein alter Turm steht in einer Ebene.Um seine Hohe zu bestimmen,steckt man in der Ebene eine horizontale Standlinie AB ab, so dass A, B und der Fußpunkt des Turms in einer Linie liegen.
Von A aus misst man zur Turmspitze den Höhenwinkel alpha von Beta aus den Höhenwinkel beta.
Wie hoch ist der Turm, und wie weit ist sein Fußpunkt von entfernt?
AB = 120
alpha = 11,8
Beta = 18.6
Skizze:
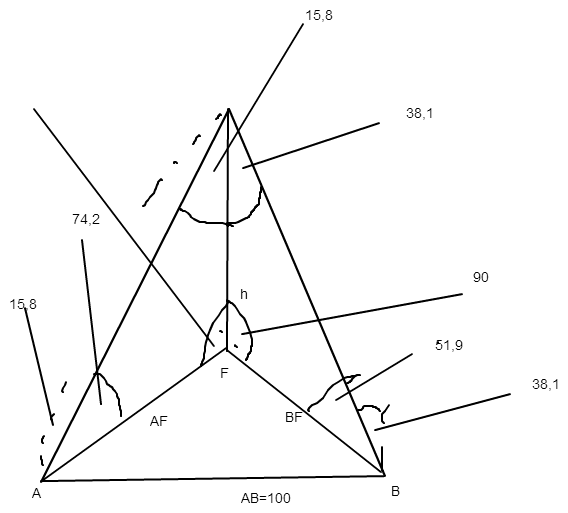
ich brauch entweder AF oder BF
danach kann ich die höhe berechnen.
ist das möglich wenn ich die Winkel 38,1 + 51,9 addiere und minus 90° das ich diesen Winkel bei Punkt B erhalte??