Bestimme die Höhe des Fernsehturms? Wie weit stehen Leo und Marko vom Turm entfernt?

Question

Leo und Marko stehen vor dem Düsseldorfer Fernsehturm. Leo sieht die Spitze des Fernsehturms unter einem Winkel von etwa 86° und Marko sieht sie unter einem Winkel von etwa 78°. Leopold und Marko stehen in einer Linie mit dem Fußpunkt des Turmes und sind 34 m voneinander entfernt.

A) Bestimme die ungefähre Höhe des Fernsehturms?

B) Wie weit stehen Leo und Marko vom Fuß des Turms entfernt?

Comments

Die Skizze laut Angaben in der Aufgabe müsste etwa so aussehen:

M ist Marko, L ist Leopold.

Marko hat einen kleineren Winkel als Leopold, steht demnach weiter weg vom Fernsehturm.

Answer 1

Zuerst gilt es, wie schon bei der vorigen Aufgabe, die fehlenden Winkel zu ermitteln:

1. 180° - 86° = 94° (an Punkt L, gestreckter Winkel ist 180°)

2. 180° = 78° + 94° + 8° (Winkelsummensatz für Dreiecke)

3. 180° = 86° + 90° + 4° (Winkelsummensatz für Dreiecke)

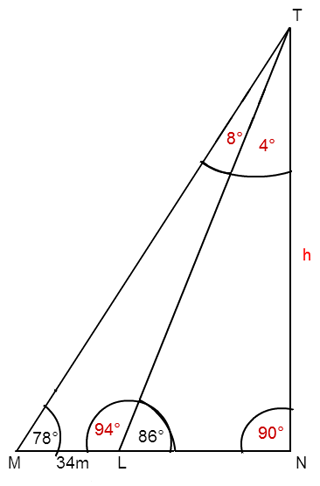
Hinweis: Skizze nicht exakt (Winkel 4° müsste kleiner als 8° gezeichnet werden).

Jetzt können wir den Sinussatz nutzen, um Strecke LT zu ermitteln:

Strecke LT ist also ≈ 238,97 m lang.

Das Dreieck LNT ist rechtwinklig, also können wir die Strecke LT als Hypotenuse ansehen und mittels Sinus die Höhe h berechnen:

sin(86°) = GK / HY

sin(86°) = h / 238,97 m     |* 238,97 m

sin(86°) * 238,97 m = h

h = sin(86°) * 238,97 m

h ≈ 238,39 m

Jetzt haben wir die ungefähre Höhe des Fernsehturms.

Unsere Skizze sieht jetzt wie folgt aus:

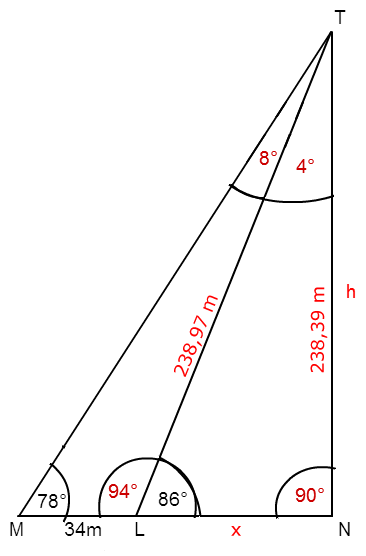
Wie du siehst, müssen wir noch x (also Strecke LN) ermitteln.

Hierzu können wir mehrere Wege gehen, nehmen wir x einfach als Ankathete und nutzen den Kosinus:

cos(86°) = AK / HY

cos(86°) = x / 238,97 m   | *238,97m

cos(86°) * 238,97 m = x

x = cos(86°) * 238,97 m

x ≈ 16,67 m

Damit steht Leo etwa 16,67 m vom Fernsehturm entfernt und Marko (16,67m + 34m) rund 50,67 m vom Fernsehturm entfernt.

Video zum Thema → Einführung Sinus und Kosinus:

Weiteres zum Themenbereich: https://www.matheretter.de/kurse/tri/

PS: Der Düsseldorfer Fernsehturm ist übrigens laut Angabe der Landeshauptstadt Düsseldorf exakt 240,5 m hoch.

Comments

danke , aber kann man diese aufgabe auch ohne den sinussatz lösen ?

---

Das ginge über den Tangens, siehe Antwort von Mitglied Unknown bei der vorigen Aufgabe.

---

Erste Gleichung aufstellen:
tan(78°) = GK / AK
tan(78°) = h / (34m+x)

Zweite Gleichung aufstellen:
tan(86°) = GK / AK
tan(86°) = h / x

Beide Gleichungen nach h umgestellt:

tan(78°) = h / (34m+x)
wird
h = tan(78°) * (34m+x)

und

tan(86°) = h / x
wird
h = tan(86°) * x


Jetzt h = h gleichsetzen:

h = h
tan(78°) * (34m+x) = tan(86°) * x

Und diese Gleichung nach x auflösen:

tan(78°) * (34m+x) = tan(86°) * x   | :tan(78°)
(34m+x) = tan(86°) * x :tan(78°)
34m+x = tan(86°):tan(78°) * x
34m+x = 3,0397 * x    | -1x
34m = 3,0397x-1x
34m = 2,0397x
2,0397*x = 34 m   |:2,0397
x = 34 m :2,0397
x ≈ 16,67