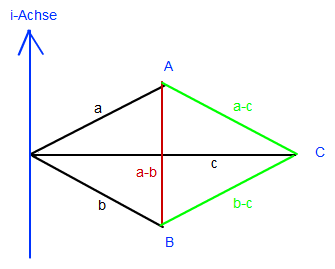
Aus der Skizze ( s.u.) entnehme ich :
Die Strecken AC und CB und AB müssen alle gleichlang sein,
also die Winkel in diesem Dreieck alle 60°.
Wegen tan(60°) = √3 / 3 geht das einfach mit
der Länge √3 also a = 3 + i √3
b= 3 - i √3 c = 6 + i*0 = 6
Dann ist | a-b| = | 2i√3 | = 2√3 | a-c| = | -3 + i√3 | = √ ( 9+3) = 2√3
und | c-b| auch 2√3