Vom Punkt T der Talstation einer Tragseilbahn aus sieht man den Gipfel G eines Berges unter dem Höhenwinkel

Question

alpha = 60. Die Seilbahn fährt zunächst a = 994 m weit unter einem Steigungswinkel von φ = 30 zur Mittelstation M. Dort ist der Winkel GMT = 135, wobei die Punkte T, M , G in einer vertikalen Ebene liegen. Wie hoch liegt der Gipfel G im Vergleich zur Talstation T?

Kann mir jemand mit der Skizze helfen?

Answer 1

Hi,

die Skizze sollte etwa so aussehen:

 

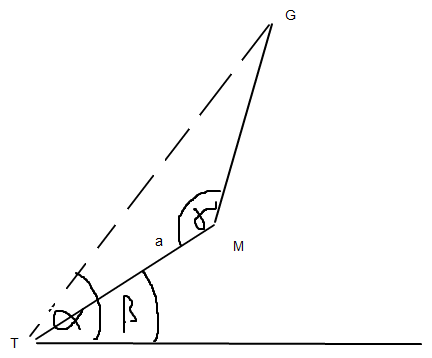
Mit dem Sinussatz, kann man direkt x (die Strecke TG) bestimmen:

994/sin(15°)=x/sin(135°)

(die 15° erhält man aus der Winkelinnensumme: 180°-30°-135°=15°)

Somit ist x=2715,66 m

 

Man kann nun hier ein rechtwinkliges Dreieck einzeichnen (Ich habe es nicht). Fälle dabei ein Lot durch G. Dann sind wir in einem rechtwinkligen Dreieck und mit

sin(60)=h/x  -> h=2351,83 m

 

Alles klar?

Grüße

Comments

Warum denn sin 60 = h/x?

Wenn ich die Höhe einzeichnen würde, dann würde es lauten: h / sin 60 = x / sin 90

Würde das auch gehen? Hast du das gemeint?

---

Das ist genau das gleiche.

sin(90°)=1

Dann kannst Du es direkt auf meine Form hin umformen ;).