Prüfung einer Tangente f(x)=1/2x²

Question

Die Tangente an eine Funktion an der Stelle x=1 schneidet die Absizisse in einem Winkel von 45°.
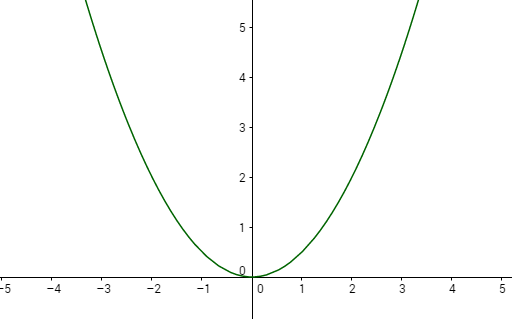
Prüfen Sie, ob f(x) = 1/2x² diese Funktion sein kann,

Mein Problem: Wie genau soll ich das jetzt darstellen, damit die Aufgabenstellung erfüllt ist?

Meine Idee: Ich habe die Funktion mal gezeichnet. Da aber der Punkt x = 1 unberührt bleibt, kann es diese Funktion nicht sein oder?

Comments

f ( x ) = 1/2 * x^2
f ´( x ) = x
f ´( 1 ) = 1 entspricht 45 °
( Tangente einmal einzeichnen )
Dies ist auch der Winkel der Tangente zu x-Achse.

---

Das mit der Ableitung verstehe ich. Nur weiß ich nicht, wie ich nun anhand dessen die Tangente einzeichnen soll. 

---

Die Tangente geht durch den Punkt
x = 1
f ( 1 ) = 1/2 * x^2 = 1/2 * 1^2 = 0.5
( 1 | 0.5 )

Die Steigung der Tangente ist 1.
Das heißt delta y / delta x = 1
Also
( 1 + 1 | 0.5 + 1 )
Vom Punkt ( 1 | 0.5 ) eins nach rechts und eins nach oben
( 2 | 1.5 )

Damit hast du 2 Punkte zum zeichnen der Tangente.
Weitere Punkte
( 1 + 2 | 0.5 + 2 )
( 3 | 2.5 )
usw

mfg Georg

---

So wäre es also korrekt? :)

---

Alles korrekt.

Answer 1

x=1 ist eine Stelle. Der Punkt dazu heißt (1/0,5). Eine Gerade durch diesen Punkt, die mit der x-Achse einen Winkel von 45° bildet hat die Steigung 1 und hat im ersten Ansatz die Gleichung  y=x+b. Das Einsetzen von (1/0,5) ergibt b=-0,5. Dann hat die Gerade die Gleichung y = x-0,5. Wenn ich diese Gerade mit der Parabel schneide, erhalte ich durch Gleichsetzen der Funktionsterme 1/2x²=x-1/2 oder x²-2x+1=0 und dann (x-1)²=0. Also ist an der Stelle  x=1 der einzige gemeinsame Punkt und die Gerade ist Tangente.