Bernoulli-Kette der Länge 3 mit .... bildet Wahrscheinlichkeitsraum. Wie zeigen?

Question

es geht um die Aufgabe auf dem Foto.





Für Wahrscheinlichkeitsraum nach Kolmogoroff muss ja gelten:

1. P≥0 für alle Ereignisse A

2. P(OMEGA) =1 für das sichere Ereignis

3. P(A und B)=P(A)+P(B) für alle unvereinbaren Ereignisse


zu 1) kann ich zeigen, dass P(0)≥0

P(0,1)=P(0)+(3 über 1)⋅p^1..... usw. >0

nur, wie soll ich 2. zeigen, wenn ich nicht weiß, wie groß p ist?

Comments

Zu 2.

A ist eine Bernoullikette der Länge 3?

Wie viele und welche gibt es da?

000

001

002

003

010

011

usw.

Addiere die Wahrscheinlichkeiten von all diesen A und schaue, ob da (wie behauptet) 1 rauskommt. Du musst dann vermutlich nur die Formeln mit p ausmultiplizieren und dann sortieren und zusammenfassen.

---

reicht für die 2 auch einfach das hier aus?

---

DAs sieht elegant aus, scheint mir aber etwas zu trivial.

Nochmals, was ist A?

Wie kommen die auf A=∅ ? Eine Bernoulli-Kette der Länge 3 ist ja nicht einfach ∅ und Omega ist auch nicht einfach A ?

---

das weiß ich leider auch nicht :( Bin auch nur ein E-Technik-Student und der Prof ist dafür bekannt, dass er Aufgaben mit fiesen Fallen stellt^^

---

Kann es sein, dass bei euch ∅ für das unmögliche Ereignis steht? Dann gibt man dem in der Tat die Wahrscheinlichkeit 0.

Schauen wir erst einmal eine Definition von Bernoulli-Ketten genauer an:

https://de.wikipedia.org/wiki/Bernoulli-Prozess

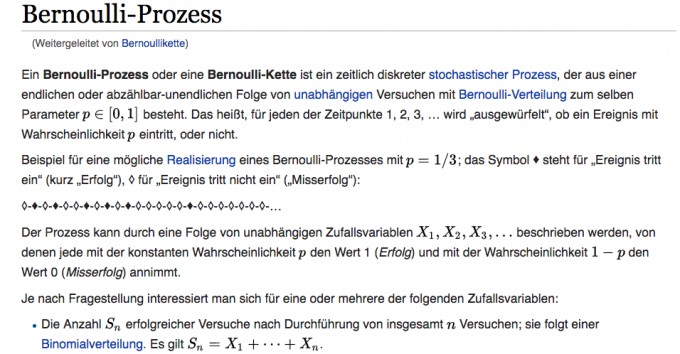
D.h. 1 sei Erfolg und 0 sei Misserfolg, dann sind folgende Ketten möglich

000 Kein Erfolg              P(kein Erfolg) = (1-p)^3

001, 010, 100 ein Erfolg       P(ein Erfolg) = 3*p(1-p)^2

011, 101, 110 zwei Erfolge      P(zwei Erfolge) = 3*p^2 * (1-p)

111 drei Erfolge        P(drei Erfolge) = p^3

Kann das sein? Schlauer ist es, wenn du das mit der Definition in deinen Unterlagen abgleichst, da ist die Wahrscheinlichkeit grösser, dass die Bezeichnungen einheitlich verwendet werden.

Bestimme dann die Wahrscheinlichkeiten der gefundenen Elementarereignisse nach deiner Formel und kontrolliere, ob da 1 rauskommt.

(1-p)^3 + 3p(1-p)^2 + 3p^2 (1-p) + p^3

= 1 - 3p + 3p^2 - p^3 + 3p(1 - 2p + p^2) + 3p^2 - 3p^3 + p^3

.....

= 1

Nach dieser Rechnung ist 2. dann hoffentlich gezeigt.