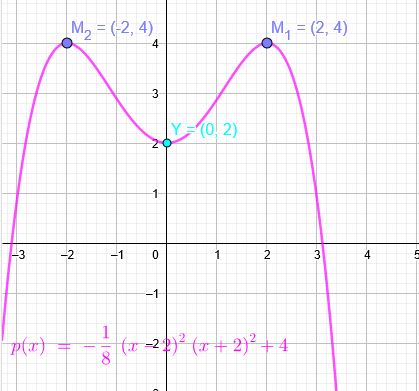
achsensymmetrische Funktion 4.Grades: verläuft durch Y\((0|2)\), Maximum bei M\((2|4)\).
\(M_1(2|4)\) ↓: \(M_1´(\red{2}|0)\) doppelte Nullstelle
Durch die Achsensymmetrie \(M_2´(-\green{2}|0)\) auch doppelte Nullstelle
\(f(x)=a(x-\red{2})^2(x+\green{2})^2\)
Y\((0|2)\) ↓: Y´\((0|-2)\):
\(f(x)=a(0-\red{2})^2(0+\green{2})^2=16a=-2\)
\(a=-\frac{1}{8}\)
\(f(x)=-\frac{1}{8}(x-\red{2})^2(x+\green{2})^2\) ↑:
\(p(x)=-\frac{1}{8}(x-\red{2})^2(x+\green{2})^2+4\)