4.Grad Achsensymmetrie \(P(2|-7)\) Hochpunkt bei \(x=1\) Bei \(x=0,5\) Tangente mit \(m=1,5\)
Achsensymmetrie bedeutet, dass auch ein 2. Hochpunkt bei \(x=-1\) ist.
Hier sind dann auch doppelte Nullstellen .
Ich verwende nun die Nullstellenform der Parabel 4.Grades:
\(f(x)=a(x-1)^2(x+1)^2=a(x^4-2x^2+1)\)
Bei \(x=0,5\) Tangente mit \(m=1,5\):
\(f'(x)=a(4x^3-4x)\)
\(f'(0,5)=a(4\cdot 0,5^3-4\cdot 0,5=-1,5a=1,5\)
\(a=-1\)
\(f(x)=-(x^4-2x^2+1)\)
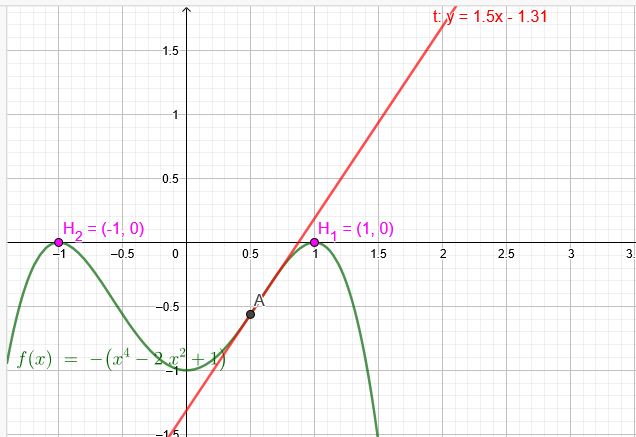
Diese Parabel hat alle geforderten Werte. Nur \(P(2|-7)\) liegt noch nicht auf dem Graphen.
Ich berechne nun den y- Wert an der Stelle \(x=2\)
\(f(2)=-(16-8+1)=-9\)
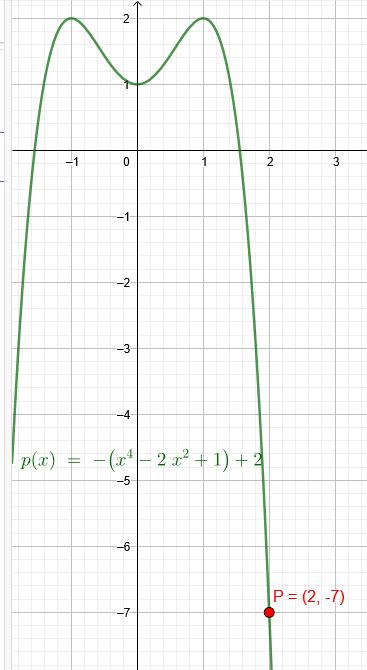
Ich muss somit den Graphen um 2 Einheiten nach oben verschieben, damit er durch \(P(2|-7)\) geht.
\(p(x)=-(x^4-2x^2+1)+2\)