Zuordnung verschiedener Graphen

Question

Servus zusammen! Ich habe folgendes Problem:

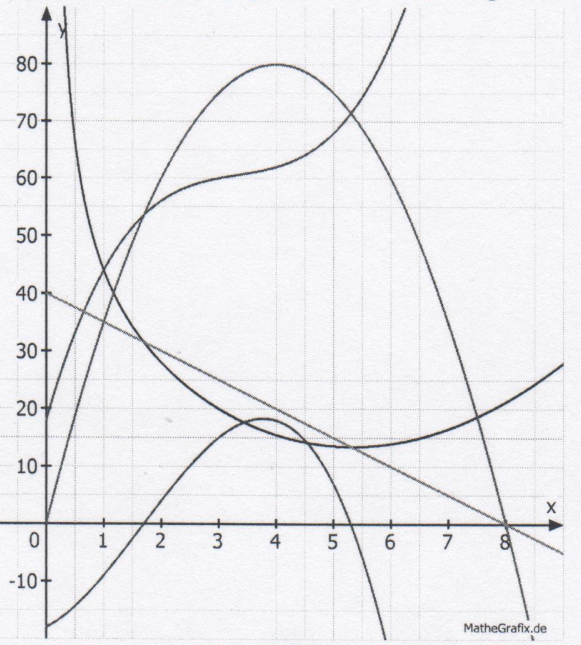
Gegeben sei folgende Abbildung (siehe Bild) der Graphen von Funktionen p, E, G, K, k .

a) Beschriften Sie die Graphen.
     (Frage: Woher soll ich wissen, welcher Graph welcher ist?)

b) Kennzeichnen Sie die folgenden Produktionsmengen:
     - Sättigungsmenge
     - Erlösmaximale Produktionsmenge
     - Break Even Point
     - Gewinnmaximale Produktionsmenge
     - Gewinngrenze 
c) Kennzeichnen Sie die folgenden Funktionswerte:
     - Höchstpreis
     - Erlösmaximum
     - Gewinnmaximum
     - Fixkosten
     - Minimale Stückkosten
     (Frage: Bei den meisten weiß ich gar nicht, wo ich was einzeichnen müsste. Vorgehensweise?)

d) Bestimmen Sie die Funktionsgleichungen von p und E.
     (Keine Ahnung wie)

Comments

Leider konnte ich mit der einen Antwort, die ich erhalten habe die Aufgabe noch immer nicht lösen.
Ich habe die Parabell, welche die Nullstellen bei 0 und 8 hat als E eingezeichnet.
Den Graphen ganz unten als G und den Graphen, der bei Y bei 18 startet als K. Ist das alles richtig?

Dann fehlen mir noch p und k. 

Desweiteren weiß ich nicht, wie ich die Punkte bei Aufgabe b) und c) erkennen soll und bei Aufgabe d) weiß ich überhaupt nicht weiter. Da kann ich ja nicht einmal raten. =(

---

Soweit ist das richtig. Die Stückkostenfunktion (klein-) k muss mit der Stelle x=0 eine Polstelle aufweisen. Es gibt nur einen Graphen, der so beschaffen sein kann. Die Preisabsatzfunktion p spiegelt den Zusammenhang zwischen dem Preis, den der Marktteilnehmer haben möchte und der Menge, die der Markt ihm dafür abnimmt wieder. Ist der Preis zu hoch (z.B. 40 GE/ME) wird er nichts verkaufen können, während er etwa bei einem Preis von 0 GE/ME sogar 8 ME verkaufen kann.

---

Jetzt habe ich alles und konnte es auch soweit nachvollziehen.

Answer 1

P(x) = 40 - 40/8·x = 40 - 5·x

E(x) = 40·x - 5·x^2

K(x) = 2/3·x^3 - 7·x^2 + 85/3·x + 19

G(x) = (40·x - 5·x^2) - (2/3·x^3 - 7·x^2 + 85/3·x + 19) = - 2·x^3/3 + 2·x^2 + 35·x/3 - 19

k(x) = (2/3·x^3 - 7·x^2 + 85/3·x + 19) / x = 2/3·x^2 - 7·x + 85/3 + 19/x

Die Graphen sehen etwa wie folgt aus

~plot~ 40-5x;40x-5x^2;2/3x^3-7x^2+85/3x+19;-2x^3/3+2x^2+35x/3-19;2/3x^2-7x+85/3+19/x;[[0|16|-20|90|]] ~plot~

Comments

Da ich die Kostenfunktion rein optisch interpoliert habe ist diese und darauf aufbauende Funktionen nicht ganz exakt. Aber graphisch macht das kaum einen Unterschied.

---

Wenn noch Dinge unklar sind dann melde dich gerne nochmals.

---

Ich denke, jetzt konnte ich es nachvollziehen.

Answer 2

Hi,

K beschreibt die Gesamtkosten und muss streng monoton steigen. Das macht nur einer der Graphen.

E beschreibt den Erlös. Bei nicht vorhandener Ausbringungsmenge ist dieser sicher 0. Auch hier gibt es nur einen Graphen.

G = E - K beschreibt den Gewinn. Auch der dazugehörende Graph kann leicht identifiziert werden.

Comments

Danke für deine Antwort! Leider bin ich bei einigen Punkten noch immer ratlos (Kommentar siehe oben). Weitere Hilfe wäre nett.