Quader mit abgetrenntem Eckteil. Innenwinkel und... der Schnittfläche?

Question

Aufgabe

Vom abgebildeten Quader (Länge 8, Breite 4, Höhe 4) wurde ein Eckteil abgetrennt.

a) gesucht sind die Innenwinkel und der Flächeninhalt der Schnittfläche ABC.

b) Welches Volumen hat das abgetrennte Eckstück?

hilfe,ich brauche das für morgen , danke

Ich verstehe das nicht mehr:(

Answer 1

Hallo Neslob,

A(4,8,0)  ,  B(2|8|4) ,  C(4|3|4)

fehlende Ecke S des Quaders:  S(4|8|4)

a) 

cos(γ)  =  cos( <) $\overrightarrow{CB}$ , $\overrightarrow{CA}$ ) = $\overrightarrow{CB}$ • $\overrightarrow{CA}$ / ( |$\overrightarrow{CB}$| • |$\overrightarrow{CA}$| )   →  γ

α analog,  β mit Winkelsumme im Dreieck.

b)

V = 1/6 • | ( $\overrightarrow{AS}$ x $\overrightarrow{BS}$ ) • $\overrightarrow{CS}$ |

Gruß Wolfgang

 

Comments

Aber warum nur CB CA? Ich habe ach mit AB AC und BC BA gerechnet.. oder?

---

Ja,  α analog, wenn man will auch β.

Den dritten Winkel erhältst du einfacher mit der Winkelsumme:  β = 180° -  α - γ 

Answer 2

Du schreibst "Ich verstehe das nicht mehr" d.h. Du hattest es mal verstanden - oder ;-)

4a) Berechne die Vektoren $\vec{AB}$ und $\vec{AC}$. Und daraus kannst Du dann z.B. den Winkel $\alpha$, also den Innenwinkel des Dreiecks ABC im Punkt A bestimmen. Es gilt $$\vec{AB} \cdot \vec{AC} =|\vec{AB}| \cdot |\vec{AC}| \cdot \cos\alpha$$ Die Vektoren sind $$A=\begin{pmatrix}4 \\ 8\\0 \end{pmatrix} \quad B=\begin{pmatrix}2 \\ 8\\ 4\end{pmatrix} \quad C=\begin{pmatrix} 4\\ 3\\ 4\end{pmatrix}$$ also $$\vec{AB} \cdot \vec{AC} = \begin{pmatrix}-2 \\0 \\ 4\end{pmatrix} \cdot \begin{pmatrix} 0\\ -5\\ 4\end{pmatrix}=\sqrt{20}\cdot \sqrt{41}\cdot \cos\alpha$$ $$\implies \cos\alpha=\frac{16}{\sqrt{20}\cdot \sqrt{41}} \approx 0,5587$$ $$\alpha \approx 56,03°$$

   

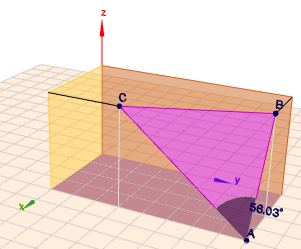
Die anderen beiden Winkel schaffst Du alleine.

Die Fläche kannst Du mit Hilfe des Kreuzprodukts berechnen. $$F=\frac{1}{2}\left| \vec{AB} \times \vec{AC} \right|=\frac{1}{2}\left| \begin{pmatrix}-2 \\0 \\ 4\end{pmatrix} \times \begin{pmatrix} 0\\ -5\\ 4\end{pmatrix} \right|=\frac{1}{2}\left| \begin{pmatrix}20 \\8 \\ 10\end{pmatrix} \right|$$ $$=\frac{1}{2}\sqrt{564}\approx 11,87$$

4b) zur Volumenberechnun kannst Du das Spatprodukt heranziehen. Die abgeschnitte Ecke bildet einen Tetraeder. Volumen eines Tetraeders ist ein sechstel des Spatprodukts der den Tetraeder aufspannender Vektoren. Ergo $$V=\frac{1}{6} \det \begin{pmatrix}0 & 0& -2\\ 0& -5& 0\\ -4& 0& 0 \end{pmatrix}=\frac{20}{3}$$Und falls Du davon noch nie etwas gehört hast, so denke Dir die fehlende Ecke E. dann betrachte die Fläche CEB mit dem Flächeninhalt $5\cdot2 /2 =5$ und die Höhe EA=4 und dann ergibt sich genauso $$V = \frac{1}{3}\cdot G \cdot h=\frac{1}{3} \cdot 5 \cdot 4=\frac{20}{3}$$

Gruß Werner

Comments

NAber ich habe 56.03 Winkel!:(

---

Oh - Du hast recht, Da habe ich die Beträge der ursprünglichen Vektoren verwendet. Der Winkel kam mir gleich zu groß vor. Dein Ergebnis von 56,03Grad ist korrekt.

---

Der letzte Winkel müsste ≈ 80,44 Grad sein, da 4: Wurzel 29 • Wurzel 20

Auf dem Bild gab’s leider einen kleinen Fehler beim letzten Winkel: (Wurzel 4+16 statt Wurzel 4•16) :D

Liebe Grüße:)