c)
Eine Tangente ist eine gerade. Wir brauchen die geradengleichung in punkt-steigungsform. Die steigung ist die ableitung an der Stelle 1.
f'(x)= -e^{2-x}
f'(1)=-e
y-y1=m(x-x1)
y-e=-e(x-1)
y=-e(x-1)+e
d)
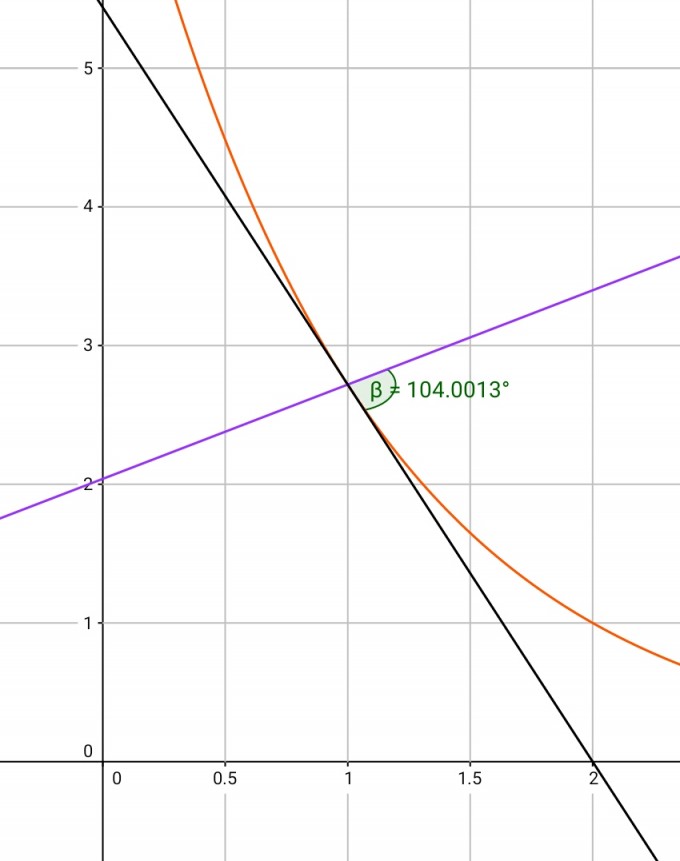
Den Schnittwinkel bestimmen wir indem wir aus den Steigungen der beiden Geraden die Schnittwinkel mit der x-Achse bestimmen und diese voneinander abziehen.
α1=arctan (e/4)=34,199°
α2=arctan (-e)=-69,802
α=α1-α2=34,199-(-69,802)=104°