Winkel Schnittwinkel (Ebenen)

Question

Ich brauche Hilfe bei a) - f). Die Punkte bei a) habe ich schon.

Das Dach eines Doppelhauses hat vier Ebenen: E₁ (Hauptdach, sichtbar), E₂ (Hauptdach, nicht sichtbar), E₃ (Gaubendach, sichtbar), E₄ Gaubendach, nicht sichtbar).

a) Ordnen Sie zunächst allen auf der Zeichnung erkennbaren Haus- und Dachecken Punkte zu und bestimmen Sie Parameter- und Normalengleichungen der Ebenen E₁ bis E₃.

b) Welchen Winkel bidet die Dachfläche E₁ mit dem Dachboden?

c) Welches Dach ist steiler, das Hauptdach oder das Gaubendach?

d) Welchen Winkel bilden E₁ und E₂ am First? Welchen Winkel bilden E₁ und E₂ in der Dachkehle?

e) Wie lautet die Gleichung der Kehlgeraden g von E₁ und E₂? Wie lang ist die Kehlstrecke? Unter welchem Winkel mündet die Kehlstrecke in die Regenrinne?

f) Sonnenlicht in Richtung des Vektors \vec{v} \( \begin{pmatrix} -1\\1\\-2 \end{pmatrix} \) erzeugt einen Schatten des 1 m hohen Lüftungsrohres mit der Spitze S (-2|6|8,8), dessen Abstand zum Dachfirst und zum Ortgang 2 m beträgt. Welchen Winkel bildet das Lüftungsrohr mit seinem Schatten?

Comments

a) - f)    ???

---

---

Kannst Du helfen?

---

Das ist eine Menge zu rechnen :-)

Schaue ggf. später danach.

---

Das wäre nett, da ich das bis morgen brauche :)

Answer 1

Hallo probe,

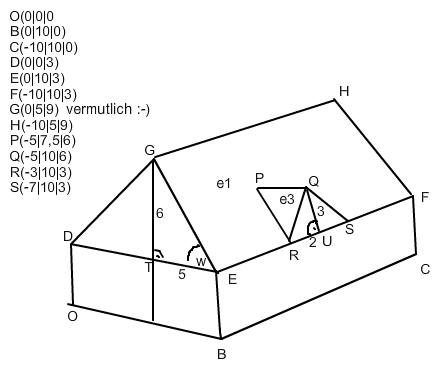
a)   Punkte vgl. oben

e1:  \(\overrightarrow{x}\) = \(\overrightarrow{OE}\) + r * \(\overrightarrow{EG}\) + s * \(\overrightarrow{EF}\)

                 Normalenvektor:  \(\overrightarrow{n}\) = \(\overrightarrow{EF}\) x \(\overrightarrow{EG}\)

        Normalengleichung:  \(\overrightarrow{n}\) * \(\overrightarrow{x}\) - \(\overrightarrow{n}\) * \(\overrightarrow{OE}\) = 0

e3:  analog

b) Winkel(e1/Dachboden):     ΔTEG:  tan(w) = 6/5  →  w ≈ 50,2°

c) Winkel(e3/Dachboden):    ΔRUQ:   tan(<) URQ) = 3/2 →   <) URQ ≈ 56,3°

                    →  e3 ist steiler als e1

d)  α = gesuchter Winkel am First:

        ΔTEG:    α/2 = 90° - w  = 39,8°  →  α = 79,6°

e)   Kehlgerade RP:   \(\overrightarrow{x}\) = \(\overrightarrow{OR}\) + r * \(\overrightarrow{RP}\)

         Länge der Kehlstrecke = | \(\overrightarrow{RP}\) | 

      Winkel ( Kehlgerade/Regenrinne) = ß:   cos(β) = \(\overrightarrow{RP}\) * \(\overrightarrow{RS}\) / (|\(\overrightarrow{RP}\)|) * |\(\overrightarrow{RS}\)|)

f)

S(-2| 6 | 8,8)

Wenn das Lüftungsrohr senkrecht verläuft, haben seine Punkte alle die y-Koordinate 6.

Da S tiefer liegt als der Dachfirst (9m), kann ich das leider nicht mit der Angabe "Abstand von S vom Dachfirst = 1m" vereinbaren, weil jeder Punkt des Dachfirstes und damit jeder Punkt senkrecht darunter die y-Koordinate 5 haben und dann in einem rechtwinkligen Dreieck sowohl die Hypotenuse als auch eine Kathete 1m lang sein müssten.

Gruß Wolfgang

            

            

Comments

Bei c) ist das Hauptdach steiler oder das Gaubendach? Kenne mich mit den Bezeichnungen nicht ganz aus.

---

Meine Fragen noch dazu:

1.) Bei c) ist das Hauptdach steiler oder das Gaubendach? Kenne mich mit den Bezeichnungen nicht ganz aus.

2.)  ΔRUQ:   tan(<) URQ) = 3/2 →   <) URQ ≈ 56,3°

Wie kommst du bei der Zeichung auf die Zahl 2?

3.)

d)  α = gesuchter Winkel am First:

Wo ist dieser Winkel in der Skizze?

4.)

Bei d) stehen 2 Fragen.... Ist die Antwort bei Frage 1 auch die für die Frage2?

5.)

zu f)

Es gilt folgendes:

Ich hoffe Du verstehst was man damit meint.

Ich erhalte dann als Winkel 75,58°. Stimmt das?

---

1)  e3 ist steiler als e1

Das Gaubendach ist also steiler.

2)  3m + 2m + 2m + 3m   =  10 m

3)  <)  DGE, also der Winkel bei G

4)  Nein

Die Dachkehle PR liegt in der Schnittgerade von  e1 und e3

In a) hast du  du die Normalenvektoren von  e1 und e3   winkel der Ebenen

Für den Schnittwinkel  γ  der Ebenen  e1 und e3 gilt: 

cos(γ) = \(\vec{n_1}\) • \(\vec{n_2}\) / ( |\(\vec{n_1}\)| · |\(\vec{n_2}\)| )

5)  g ist die Gerade durch s in Richtung des Sonnenlichts.Vergessen wir mal die Angaben zu den Abständen in f).  P ist das untere Ende des Lüftungsrohrs 1m tiefer als S in der Ebene e1.

     Dann ist  S₂ der Schnittpunkt von  g und e1  und damit der Schattenpunkt von S in e1