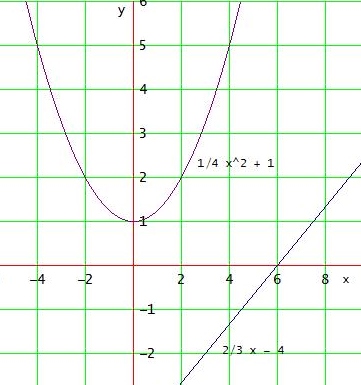
f(x) = 2/3 x - 4
Dmax = ℝ denn man kann jede reelle Zahl für x einsetzen, ohne dass es beim Ausrechnungen Probleme gibt.
Bildmenge = ℝ denn bei den Punkten von f kommt jede reelle Zahl als y-Wert vor
Die Funktion ist streng monoton steigend denn ein größerer x-Wert hat immer auch einen größeren y-Wert
f ist weder nach unten noch nach oben beschränkt, weil die Funktionswerte y beliebig groß bzw. klein werden.
limx→ ∞ f(x) = ∞ ; limx→ - ∞ f(x) = - ∞
f/x) = 1/4 x2 + 1
Dmax = ℝ denn man kann jede reelle Zahl für x einsetzen, ohne dass es beim Ausrechnungen Probleme gibt.
Bildmenge = [ 1/4 ; ∞ [ denn bei den Punkten von f kommt jede reelle Zahl ≥ 1/4 als y-Wert vor.
Die Parabel hat ihren Scheitelpunkt (tiefster Punkt) in (0|1). Sie ist streng monoton fallend in ] - ∞ ; 1/4 ] und streng monoton steigend in [ 1/4 ; ∞ [
f ist durch y = 1/4 nach unten beschränkt. Nach oben ist sie nicht beschränkt.
limx→ ∞ f(x) = limx→ - ∞ f(x) = ∞
Gruß Wolfgang