Liegt der Punkt P im Körper (Aufgespannte Pyramide)?

Question

Hallo erstmal.Diese Aufgabe wurde hier schon ein paar mal gestellt, aber ich habe noch ein paar Fragen dazu bzw. wie ich meine persönliche Lösung erklären kann.
Aufgabe: Liegt der Punkt P(1,2,2) in dem von den Punkten A(3,0,0);B(0,12,0);C(0,0,6)und D(0,0,0) aufgespanten Pyramide ?
Meine Lösung: Ich stelle den Punkt P mit hilfe der Linearkombination dar=>
$$ \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}=a\begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}+b\begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix}+c\begin{pmatrix} 0 \\ 0 \\ 6 \end{pmatrix}\quad =>a=\frac { 1 }{ 3 } ,\quad b=\frac { 1 }{ 6 } ,\quad c=\frac { 1 }{ 3 } \\ $$

Da a+b+c<1 und >0 liegt P in der Pyramide.
Nun meine Frage warum gilt dies? bzw. wie lässt sich das erklären? Könnte mir das jemand einmal genau erklären?
Viel dank im voraus

Answer 1

Kannst du die 3 Vektoren und die aufgespannte Pyramide in meiner Skizze erkennen?

Dann ist schon mal ersichtlich, dass a, b und c nicht negativ sein können, wenn der Punkt innerhalb der Pyramide liegen soll.

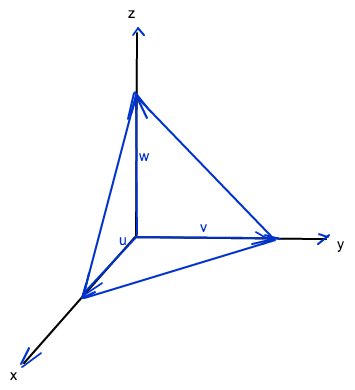
Und ist dir klar, dass OP = a* u , mit 0 ≤ a ≤ 1 die Ortsvektoren der Punkte auf einer Pyramidenkante sind?

Nun ein Punkt auf einer anderen Kante:

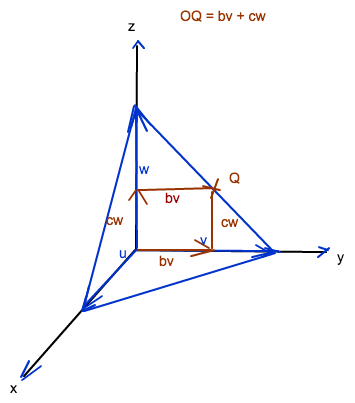
Gemäss Strahlensatz gilt | cw| : | w| = ( | v - bv | ) : | v|

Mit den Längen der Vektoren kürzen:  c : 1 = 1 - b : 1

c = 1- b

b+c = 1 . Für die Kante.

Das ergibt für alle Punkte die auf der rückseitigen Fläche der Pyramide liegen:

OQ = bv + cw , mit b+c ≤ 1 und b und c nicht negativ.

Nun noch eine Skizze für einen allgemeinen Punkt P auf der schiefliegenden Pyramidenseite

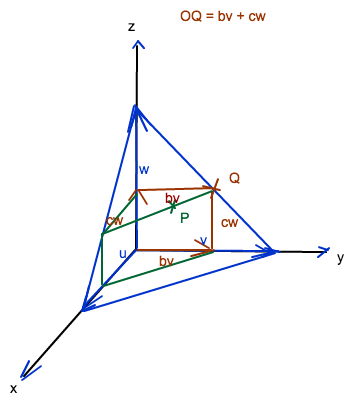
Hier ist nun a nicht mehr 0 und die kannst (wenn du die Skizze grösser machst im grün-roten Dreieck den Strahlensatz benutzen.

Es ergibt sich für den Ortsvektor von P, dass a + (b+c) = 1.

Für Punkte im Innern (inklusive Seitenkante) der Pyramide muss dann gelten a + b + c ≤ 1, sowie immer noch a≥0, b≥0 und c≥ 0.