zur Berechnung der Höhe habe ich die wichtigsten Längen skizziert
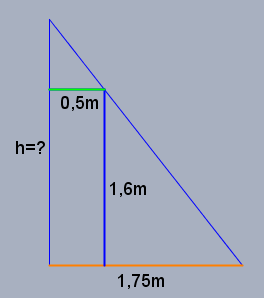
nach Strahlensatz ist $$\frac{h}{1,6\text{m}}=\frac{1,75\text{m}}{1,75\text{m}-0,5\text{m}}=\frac{1,75}{1,25} \quad \Rightarrow \quad h=2,24\text{m}$$
Die Mantelfläche eines Kegels ist \(M=rs\pi\), \(\quad r\) ist hier \(r=1,75\text{m}\) und \(s=\sqrt{h^2+r^2}\). damit ist M: $$M=r\sqrt{h^2+r^2} \pi= 1,75\text{m} \sqrt{(2,24\text{m})^2+(1,75\text{m})^2} \cdot \pi \approx 15,63\text{m}^2$$
Das Gewicht der Säule ist gleich dem Volumen V mal des spezifischen Gewichts. Das spezifische Gewicht ist die spezifische Masse bzw. Dichte \(\rho=2,6\frac{\text{t}}{\text{m}^3}\) mal der Erdbeschleunigung g. Zusammen \(G=V\cdot \rho \cdot g\). Das Volumen ist gleich dem Volumen des Zylinders \(V_Z\) minus dem Volumen der Halbkugel \(\frac{1}{2}V_K\).$$G=\left( \pi h{(r_Z)}^2- \frac{1}{2}\cdot \frac{4}{3}\pi {(r_K)}^3\right) \rho \cdot g $$ $$ =\pi\left(1,6\text{m} (0,5\text{m})^2 - \frac{2}{3}(0,3\text{m})^3 \right) 2,6 \frac{1000\text{kg}}{\text{m}^3} \cdot 9,80665 \frac{\text{m}}{\text{s}^2}$$ $$\approx 27,23kN$$Gruß Werner
