Hallo Leila,
eine kleine Skizze eines gleichschenkligen Dreiecks hilft wahrscheinlich:
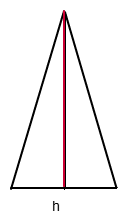
Ein gleichschenkliges Dreieck hat 2 gleichlange Seiten und eine 3. Seite mit einer anderen Länge. Hier habe ich
dummerweise die Grundseite als h gekennzeichnet, gemeint ist natürlich g. Die Höhe hg ist die rote Linie.
Nun sind die "kleinen" Dreiecke links und rechts jeweils rechtwinklig, womit Pythagoras ins Spiel kommt.
a) g = 16cm, hg = 150cm.
Die kleinen Dreiecke haben also als Katheten 8cm (die Hälfte von 16cm) und 150cm (die Höhe). Die Schenkel S sind dann jeweils die Hypotenuse. Gleichung:
S^2 = 8^2 + 150^2
S = √(64 + 22500) ≈ 150,21cm
b) g = 1,2m = 120cm, hg = 17cm
S^2 = 60^2 + 17^2
S = √(3600 + 289) ≈ 62,36cm