Stetigkeit in einem Punkt nachweisen

Question

Ich schreibe bald eine Matheklausur und verzweifele an der  folgenden Aufgabe

Untersuchen Sie, ob die Funktion f mit

f: {x ∈ R Ι ΙxΙ≤4} --> R mit x --> 

Ιx+3Ι-3   für x ∈ [-4,0] 

√x           für x ∈ [0,4] 

auf [-4,4] stetig ist.

Wäre Ihnen für einen Lösungsweg sehr dankbar.

Comments

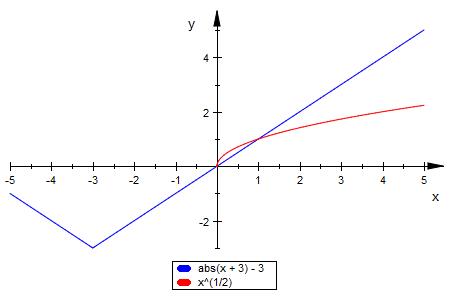
Die Fragestellung ist ob die geteilte Funktion

| x + 3 | - 3 für x zwischen-4 und 0
und
Wurzel ( x ) für x zwischen 0 und +4 stetig ist

Die Teilfunktionen sind jeweils stetig.

Ist jetzt an der Schnittstelle auch

t1 ( 0 ) = t2 ( 0 )
| 0 + 3 | - 3 = √ ( 0 )
0 = 0

Die Funktion  ist insgesamt stetig.
Die Funktion weist keine Lücke oder Sprung auf
links ist blau gültig; rechts rot

Answer 1

Hi,

Die Teilfunktionen sind für sich je stetig. Deshalb musst Du nur die Stelle x = 0 untersuchen.

|0+3|-3 = 0

√0 = 0

Diese stimmen überein und damit ist die Funktion f als ganzes stetig.

Grüße