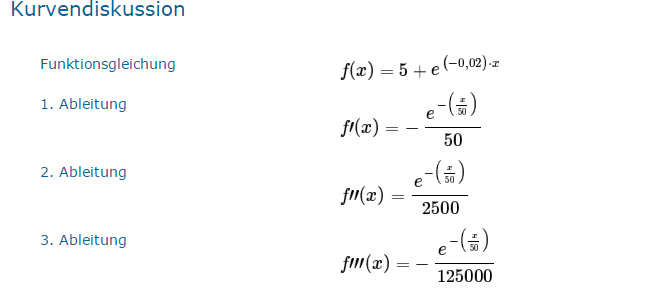Ableitungen sowie Zusammenfassen e Funktion

Question

stehe grade etwas auf dem Schlauch wegen einer Ableitung, würde mich über eure Hilfe sehr freuen Aufagbe sieht wie folgt aus.

Bestimme Ableitung von f(x)= 5+ e^{-0,02*x} sowie h(x)= 40-25*e^{-0,1*x}

finde irgendwie nicht den richtigen Ansatz habe dann die Ableitung angeguckt im Internet davon und verstehe nicht gänzlich wie man darauf kommt weil f'(x) soll angeblich = -(e^{-x/50}/50) sein. Würde mich sehr freuen wenn mir jemand sagen kann wie man darauf kommt.  (Bild der Ableitung sonst im Anhang)

Desweiteren wollte ich fragen wie man diese Funktion weiter auflösen würde:

(5+e^{-0,02*x}) * (40-25*e^{-0,1*x}) also praktisch von den oben gennanten Funktonen f(x)*h(x)

Bedanke mich im Voraus für die Hilfe (:

Comments

Unbedingt merken. Wird immer wieder gebraucht.

( e^term ) ´ = e^term *  ( term ´ )

e^-0,02*x

term = -0.02 * x
term ´ = -0.02

( e^-0,02*x ) ´ = e^-0,02*x * ( -0.02 )

Answer 1

h(x)= 40-25*e^-0,1*x. Beim Ableiten fallen konstante Summande weg und b·e^ax  wird zu b·a·e^ax.    b =-25 und a = -0,1. dann ist a·b= 2,5=5/2. Also h'(x)= 2,5*e^-0,1*x.

Comments

Hmm.. also doch praktisch ganz normale Verkettung nur das der Summand wegfällt bei der Ableitung.. war mir nicht mehr ganz sicher mich hat die Ableitung auf dem Screen verwirrt..

demnach müsste dann ja aber f(x)= 5+e^{-0,02*x} = f'(x)= -0,02*e^{-0,02*x} sein oder mache ich jetzt einen Denkfehler?

Vielen Dank für die Hilfe (:

---

Dein f '(x) ist richtig

---

Hmm, okay danke an dich.. dann wird die Ableitung auf dem Screenshot wohl einfach eine umgestellte Variante von dem Sein nehme ich an.. war etwas verwirrend danke für die schnelle Hilfe (:

Answer 2

Es ist $$ 0.02 = \dfrac {1}{50} $$

Comments

Ist mir klar, komme nur trotzdem nicht darauf wie man auf so eine Ableitung kommt.. zumindest nicht nach welcher Regel diese Ableitung zustande kommt.