ich habe eine Frage zur Konvergenz von Reihen.
Eine Reihe konvergiert ja, wenn die Folge über ihre Partialsummen konvergiert.
Wenn ich also die Reihe ∑1/n habe müsste doch als Reihenwert 2 rauskommen ? (für n ∈ ℕ).
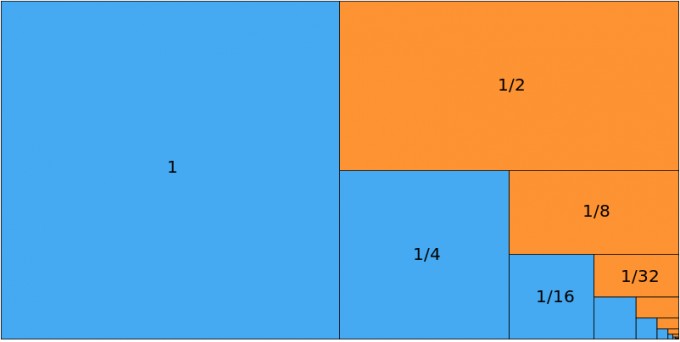
wie auf der Grafik zu sehen..
Allerdings ist die Reihe über 1/n ja die harmonische Reihe, welche divergiert ich verstehe hier nicht ganz weshalb sie divergiert wenn der Grenzwert doch offensichtlich bei 2 liegt.
Ist damit jede Reihe, welche eine Nullfolge ist automatisch divergent und wenn ja weshalb ?