Wir betrachten die Funktion \(f(x)=\dfrac{1}{x}\). Der Flächeninhalt unter der Kurve mit der unteren Grenze \(a=1\) ist gegeben durch: $$\int_{1}^{\infty}{\dfrac{1}{x}}\mathrm{dx}$$ Berechnen wir diesen schrittweise, so ergibt sich: $$\int_{1}^{\infty}{\dfrac{1}{x}}\mathrm{dx}\approx\underbrace{0.69}_{\int_{1}^{2}{\frac{1}{x}}\mathrm{dx}<1}+\underbrace{0.4055}_{\int_{2}^{3}{\frac{1}{x}}\mathrm{dx}<\frac{1}{2}}+\underbrace{0.29}_{\int_{3}^{4}{\frac{1}{x}}\mathrm{dx}<\frac{1}{3}}+...$$
Schauen wir uns folgende Grafik an: 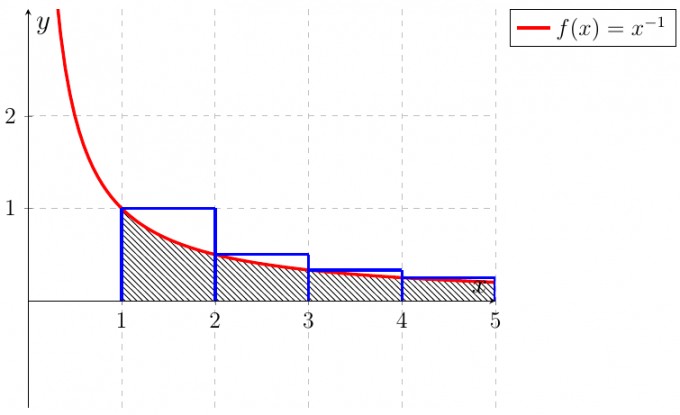
Die blauen Kästen besitzen die Fläche \(1\cdot 1=1\), \(1\cdot \frac{1}{2}=\frac{1}{2}\), \(1\cdot \frac{1}{3}=\frac{1}{3}\) usw.. In Summe also:
$$1+\dfrac{1}{2}+\dfrac{1}{3}+... = \sum\limits_{k=1}^{\infty}{\dfrac{1}{k}}$$ Man sieht bereits, dass der Flächeninhalt der Teilstücke unter der roten Kurve kleiner ist als die entsprechenden Reihenglieder. Doch welchen Wert nimmt \(\int_{1}^{\infty}{\frac{1}{x}}\mathrm{dx}\) an? Wir berechnen den Wert dieses uneigentlichen Integrals durch: $$\int_{1}^{\infty}{\frac{1}{x}}\mathrm{dx}=\lim_{k\rightarrow\infty}{\int_{1}^{k}{\frac{1}{x}}\mathrm{dx}} =\lim_{k\rightarrow\infty}{\left[\ln{(x)}\right]_{1}^{k}}=\lim_{k\rightarrow\infty}{\underbrace{\ln(k)}_{\infty}-\underbrace{\ln(1)}_{0}}=\infty$$ Und wenn der Flächeninhalt der grau schattierten Fläche schon unendlich ist, dann trifft das auf den Flächeninhalt der blauen Kästen allemal zu! Hilft Dir dieser Erklärungsansatz?