Hallo Laura,
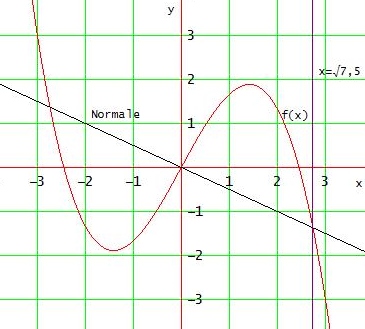
f(x) = 2x - 1/3 · x3
da nur ungerade Exponenten bei x vorkommen, ist f symmetrisch zum Ursprung
f '(x) = 2 - x2
f "(x) = -2x = 0 → Wendepunkt W(0|0)
Die Tangente in W hat die Steigung mT = f '(0) = 2
Die Normale steht dort senkrecht zur Tangente → mN = -1 / mT = - 1/2
→ Normalengleichung y = - 1/2 · x
Schnittstellen zwischen dem Graph von f und der Normalen:
2x - 1/3 · x3 = - 1/2 x ⇔ 5/2 x - 1/3 x3 = 0 ⇔ x * ( 5/2 - 1/3 x2) = 0 ⇔ x = 0 oder 5/2 - 1/3 x2 = 0
⇔ x2 = 15/2 ⇔ x = ± √(7,5)
Wegen der Symmetrie von f zum Ursprung beträgt die gesuchte Fläche
A = 2 * 0∫√(7,5) ( 2x - 1/3 · x3 - (-1/2x) ) dx = 2 * 0∫√(7,5) ( 5/2·x - x3/3) dx
= 2 * [ 5/4 x2 - x4/12 ]0√(7,5) = 2 * 75/16 = 9,375
Gruß Wolfgang