Hallo, ich habe dazu auch eine Frage:
Ich habe zwei Unbekannte und mehrere Formeln. Mir sind nicht mehr so gut die mathematischen Gesetze präsent, als dass ich das sicher hinbekommen könnte, denke ich:
Zwei rote Farbproben haben die Werte: Wie hoch sind ∆E* und ∆H*?
L*1 = 54,5, C*1 = 38,4, h1 = 18
L*2 = 52, C*2 = 35, h2 = 21
∆C* = C*2 - C*1

Text erkannt:
\( \Delta \mathrm{E}^{*}{ }_{94} \approx \sqrt{\left(\Delta L^{*}\right)^{2}+\left(\frac{\Delta C^{*}}{1+0,045 \cdot C_{1}^{*}}\right)^{2}+\left(\frac{\Delta H^{*}}{1+0,015 \cdot C_{2}^{*}}\right)^{2}} \)
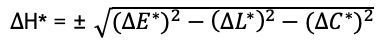
Text erkannt:
\( \Delta \mathrm{H}^{*}=\pm \sqrt{\left(\Delta E^{*}\right)^{2}-\left(\Delta L^{*}\right)^{2}-\left(\Delta C^{*}\right)^{2}} \)
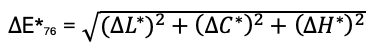
Text erkannt:
\( \Delta \mathrm{E}^{*}{ }_{76}=\sqrt{\left(\Delta L^{*}\right)^{2}+\left(\Delta C^{*}\right)^{2}+\left(\Delta H^{*}\right)^{2}} \)
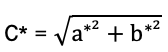
Text erkannt:
\( \mathrm{C}^{*}=\sqrt{\mathrm{a}^{*^{2}}+\mathrm{b}^{*^{2}}} \)
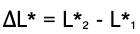
Text erkannt:
\( \Delta L^{*}=\left\lfloor^{*}{ }_{2}-\left\lfloor^{*}{ }_{1}\right.\right. \)
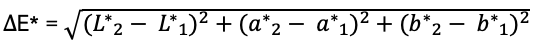
Text erkannt:
\( \Delta \mathrm{E}^{*}=\sqrt{\left(L^{*} 2-L_{1}^{*}\right)^{2}+\left(a_{2}^{*}-a_{1}^{*}\right)^{2}+\left(b_{2}^{*}-b_{1}^{*}\right)^{2}} \)

Text erkannt:
\( \mathrm{h}=\arctan \frac{b^{*}}{\mathrm{a} *} \)
Ich muss die Formeln irgendwie ineinander packen und dann nach der letzten Unbekannten auflösen. Ich habe schon einmal etwas angefangen:
 Aber wenn ich jetzt überlege, dass ich nach b* oder a* auflösen muss, weiß ich nicht genau, wie ... :)
Aber wenn ich jetzt überlege, dass ich nach b* oder a* auflösen muss, weiß ich nicht genau, wie ... :)
Kann mir bitte jemand auf die Sprünge helfen?
Danke
Text erkannt:
\( \mathrm{C} *=\sqrt{\mathrm{a}^{*^{2}}+\mathrm{b}^{*^{2}}} / \sqrt{=} \sqrt{\mathrm{C} *}=\mathrm{a}^{*}+\mathrm{b}^{*} /-\mathrm{b}^{*}=\sqrt{\mathrm{C} *}-\mathrm{b}^{*}=\mathrm{a}^{*} \quad \mathrm{a}^{*^{2}}+\mathrm{b}^{*^{2}}=\mathrm{c}^{*^{2}} \)
\( \mathrm{~h}=180(360)+\arctan \frac{b *}{\mathrm{a}^{*}}=\arctan =\tan \mathrm{h}=\frac{b *}{\mathrm{a} *} / \cdot \mathrm{a}^{*}=\tan \mathrm{h} \cdot \mathrm{a}^{*}=\mathrm{b}^{*} \)
\( \mathrm{C}^{*}=\sqrt{(\sqrt{\mathrm{C} *}-\mathrm{b} *)^{2}+\left(\tan h \cdot(\sqrt{\mathrm{C} *}-\mathrm{b} *)^{2}\right.}= \)
\( \sqrt{\mathrm{C} *}-\left(\tan \mathrm{h} \cdot \mathrm{a}^{*}\right)=\mathrm{a}^{*} \)
\( \tan \mathrm{h} \cdot\left(\sqrt{\mathrm{C} *}-\mathrm{b}^{*}\right)=\mathrm{b}^{*} /\left(\sqrt{\mathrm{C} *}-\mathrm{b}^{*}\right)=\tan \mathrm{h}=\frac{b *}{\sqrt{\mathrm{C} *}-\mathrm{b} *} / \cdot \sqrt{\mathrm{C} *}=\tan \mathrm{h} \cdot \sqrt{\mathrm{C} *}=\frac{b *}{-\mathrm{b} *}= \)
Text erkannt:
\( \Delta \mathrm{E}^{*}{ }_{94}=\sqrt{\left(\frac{\Delta L^{*}}{S_{L} \cdot k_{L}}\right)^{2}+\left(\frac{\Delta C^{*}}{S_{C} \cdot k_{C}}\right)^{2}+\left(\frac{\Delta H^{*}}{S_{H} \cdot k_{H}}\right)^{2}} \)