Bei einem schräg geworfenen Ball kann die Flugbahn mit einer Parabel beschrieben werden...

Question

Bei einem schräg geworfenen Ball kann die Flughbahn durch die Parabel f(x)= -0,1x² + 0,5x +1,8 beschrieben werden.

Hierbei entspricht x(in Metern) der horizontalen Entfernung vom Abwurfpunkt und f(x) (in Metern) der Flughöhe des Balles über dem Boden.

a) in welcher Höhe wurde der Ball abgeworfen?

b) Welche Definitionsmege ist für die zugehörige Funktion sinnvoll?

c) Bestimmen Sie die maximale Flughöhe des Balles.

d) Bearbeiten sie die Teilaufgaben b) und c), wenn der Ball von der Höhe h abgeworfen wird.

Ich freue mich sehr über antworten.

 

Answer 1

Hi,

a) In welcher Höhe wird der Ball abgeworfen?

Das geschieht bei x=0 -> f(0)=1,8

Der Ball wird in einer Höhe von 1,8m abgeworfen.

 

b) Sinnvolle Definitionshöhe ist der Teil, welcher sich im ersten Quadranten befindet:

 

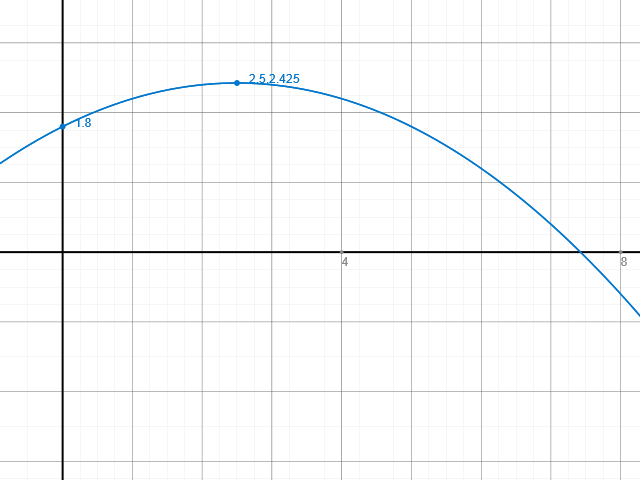
Also alles von 0 bis etwa 8, da wo die Kugel auf dem Boden aufschlägt. Um es genau zu berechnen:

-0,1x^2+0,5x+1,8=0 |:(-0,1)

x^2-5-18=0      |pq-Formel

x₁=-2,42 und x₂=7,42

 

Ein sinnvoller Definitionsbereich ist also für 0≤x≤7,42 gegeben.

 

c)

Die maximale Höhe lässt sich über die Scheitelpunktformel errechnen oder über die erste Ableitung. Ich wähle letzteres:

f'(x)=-0,2x+0,5=0

0,2x=0,5

x=2,5

 

An der Stelle x=2,5 liegt ein Extremum vor, das unser Hochpunkt ist (im Zweifelsfalle mit zweiter Ableitung überprüfen).

Der Ball ist dabei in einer Höhe von f(2,5)=2,425 zu finden (siehe auch Schaubild).

 

Grüße

Comments

d) Nicht abhängig von 1,8 m, sondern von einer beliebigen Höhe h, hat man halt eine Variable in der ganzen Rechnung.

 

Die vormalige b)

-0,1x²+0,5x+1,8=0

wird zu -0,1x²+0,5x+h=0

Da wie oben die pq-Formel anwenden.

 

Die vormalige c)

Die Stelle x=2,5 ist immer dieselbe. Es muss also nur f(2,5) bestimmt werden und schon hat man den neuen Hochpunkt bei H(2,5|f(2,5)).

---

Vielen Dank ich werde es jetzt erstmal durchgehen und dir dann berichten

---

Geht klar. Bin da ;).

---

Wie rechne ich c)

Ich habe es jetzt mit der Scheitelpunktform gemacht und das hier soweit raus:

y=x^2+5x-18

x^2+5x+2,5^2-2,5^2-18

(x+2,5)^2 -24,25


Ist das richtig und wenn ja wo lese ich jetzt die maximale Flughöhe ab?

Danke:)

---

Vorsicht. Du hast mit y=x²+5x-18 gearbeitet. Das ist aber nicht die originale Funktion (abgesehen von dem Vorzeichenfehler). Du musst den Faktor 0,1 mit berücksichtigen!

 

y=-0,1(x²-5x-18)

Nun kannst Du in der Klammer so vorgehen, wie Du es vorgemacht hast.

=-0,1((x²-5x+2,5²)-2,5²-18)

=-0,1((x-2,5)^2-2,5^2-18)

=-0,1((x-2,5)^2-24,25)

=-0,1(x-2,5)^2+0,1*24,25

=-0,1(x-2,5)^2+2,425

 

Jetzt kann man das Ergebnis direkt ablesen. In der Klammer steht der x-Wert (verkehrtes Vorzeichen) und als Summand hintendran steht der y-Wert

-> H(2,5|2,425)

 

Einverstanden?
 

---

Gerne :)        .

---

Wie rechnet man d? 

---

Du machst die gleiche Rechnung nochmals, aber statt 1,8 m nimmst Du einfach h. Hast also einen Parameter ;).

---

allerdings habe ich doch dann eine variable in der pq-formel. wie löse ich das denn ?

---

Betrachte h als eine Zahl und schlepp sie mit. Probier es mal ;).