Schreiben Sie die Teilmenge {x∈R: x≤4+√x-2} als Vereinigung von Intervallen

Question

Hilfe, ich weiß nicht wie ich das schreiben soll:

Schreiben Sie die folgende Teilmenge von R als Vereinigung von Intervallen

{x∈R: x≤4+√x-2}

.

Answer 1

Ich nehme an, das Wurzelzeichen geht bis über die 2 . Dann ist x auf jeden Fall  x  ≥2

x≤4+√(x-2)                    |-4

x -4 ≤ √(x-2)                    |²                                  

 Im Intervall von [2,4] ist der linke Term kleiner als oder =0 deshalb gilt die Ungleichung

Für x>4 rechne ich weiter

x -4 ≤ √(x-2)                    |²                   

(x -4)²  ≤ x -2

x² - 8x + 16 ≤ x -2

x² - 9x + 18 ≤ 0

Links: Nach oben geöffnete Parabel. Ungleichung ist erfüllt zwischen den Nullstellen.

Nullstellen =

Lsg. der Gleichung:         x_1,2 = 1/2 * (9 ± √ (81 - 4*18)) = 1/2 * (9 ± 3) 

x₁ = 3, x₂ = 6

x² - 9x + 18 ≤ 0 gilt in [3,6] geschnitten mit [4, unendlich] = [4,6]

Total

x≤4+√(x-2)      gilt in [2,4] u [4,6]  = [2,6]

 

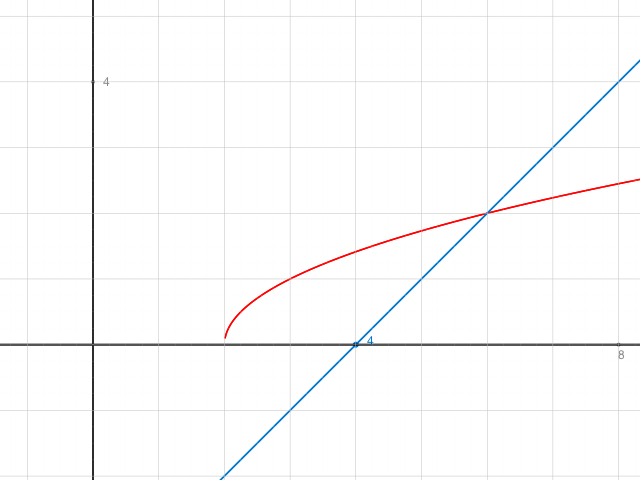
Probe: Graph dieser Ungleichung x -4 ≤ √(x-2)     

blau: linke Seite. rot: rechte Seite.

Im Intervall von 2 bis 6 verläuft die blaue Kurve unter der roten.

 

 

Comments

cool danke, dann war mein ansatz doch richtig, aber du hast nicht geschrieben, wie die schreibweise ist??

---

 

Doch: {x∈R: x≤4+√x-2} =  [2,4] u [4,6]  = [2,6]    sollte genügen

u steht hier für die Vereinigung von Intervallen

---

was ich noch nicht so ganz verstehe ist das:

x2 - 9x + 18 ≤ 0 gilt in [3,6] geschnitten mit [4, unendlich] = [4,6]

wie kommst du auf unendlich? danach hast du ja im intervall die 6 drin, warum?

---

Ich rechne ja nur weiter für x>4 und das ist das Intervall [4, unendlich[  . Achtung: rechts offenes Intervall.

Nur so ist sicher, dass sich beim Quadrieren

also hier : x -4 ≤ √(x-2)                    |²       

das Ungleichheitszeichen nicht dreht. Wurzeln sind gemäss Definition ≥0.

x -4 ≤ √(x-2)                    |²       

 

Die Fälle in denen x-4 <0 ist habe ich im ersten Teil schon behandelt.